题目内容
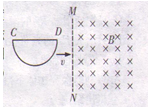
【题目】如图所示,轨道分粗糙的水平段和光滑的圆弧段两部分,O点为圆弧的圆心,半径![]() 。两轨道之间的宽度为0.5m,匀强磁场方向竖直向上,大小为0.5T。质量为0.05kg、长为0.5m的金属细杆置于轨道上的M点,当在金属细杆内通以电流强度恒为2A的电流时,金属细杆沿轨道由静止开始运动。已知金属细杆与水平段轨道间的滑动摩擦因数
。两轨道之间的宽度为0.5m,匀强磁场方向竖直向上,大小为0.5T。质量为0.05kg、长为0.5m的金属细杆置于轨道上的M点,当在金属细杆内通以电流强度恒为2A的电流时,金属细杆沿轨道由静止开始运动。已知金属细杆与水平段轨道间的滑动摩擦因数![]() ,N、P为导轨上的两点,ON竖直、OP水平,且MN=1m,g取10m/s2,则下列说法错误的是()
,N、P为导轨上的两点,ON竖直、OP水平,且MN=1m,g取10m/s2,则下列说法错误的是()

A. 金属细杆开始运动时的加速度大小为4m/s2
B. 金属细杆运动到P点时的速度大小为![]()
C. 金属细杆运动到P点时的向心加速度大小为8m/s2
D. 金属细杆运动到P点时对每一条轨道的作用力大小为0.9N
【答案】C
【解析】试题分析:根据牛顿第二定律得:金属细杆开始运动时的加速度大小为:![]() ,故A错误;设金属细杆运动到P点时的速度大小为v,从M到P过程,由动能定理得:
,故A错误;设金属细杆运动到P点时的速度大小为v,从M到P过程,由动能定理得:![]()
则得:![]() ,故B错误;金属细杆运动到P点时的向心加速度大小为
,故B错误;金属细杆运动到P点时的向心加速度大小为![]() ,故C错误;在P点,设每一条轨道对细杆的作用力大小为N,由牛顿第二定律得:
,故C错误;在P点,设每一条轨道对细杆的作用力大小为N,由牛顿第二定律得:![]() ,代入数据解得:
,代入数据解得:![]() ,由牛顿第三定律得细杆在P点对每一条轨道的作用力大小为
,由牛顿第三定律得细杆在P点对每一条轨道的作用力大小为![]() ,故D错误。
,故D错误。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目