题目内容
18.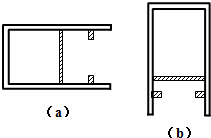 如图(a),一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2.0×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa.现将气缸缓慢转动到开口向下竖直放置,如图(b)所示,取g=10m/s2.求:
如图(a),一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2.0×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa.现将气缸缓慢转动到开口向下竖直放置,如图(b)所示,取g=10m/s2.求:(1)活塞与气缸底部之间的距离;
(2)图(b)中,要使活塞下降到与卡环接触位置则封闭 气体的温度至少为多少?
(3)加热缸中气体到540K时封闭气体的压强为多少?
分析 (1)气缸水平放置时,封闭气体的压强等于大气压强,当气缸竖直放置时,封闭气体的压强等于大气压强加活塞重力产生的压强,由于两种情况下气体的温度保持不变,根据等温变化求出此时气体的体积,根据气体的体积可以求出活塞与气缸底部之间的距离;
(2)气体经历等压变化,根据盖-吕萨克定律列式求解.
(3)由360K到540K为等容变化,列出状态参量,由查理定律即可求出.
解答 解:(1)气缸水平放置时,封闭气体的压强:${P_1}=1.0×{10^5}Pa$ 体积:V1=24S
当气缸竖直放置时,封闭气体的体积:V2=L2S
封闭气体的压强:${P_2}={P_0}-\frac{mg}{S}=(1.0×{10^5}-\frac{40}{{2×{{10}^{-3}}}})Pa=0.8×{10^5}Pa$
由于等温变化,有${P_1}{V_1}={P_2}V_2^{\;}$
得 ${L_2}=\frac{{{P_1}{V_1}}}{{{P_2}S}}=\frac{{1.0×{{10}^5}×24S}}{{0.8×{{10}^5}S}}cm=30cm$
(2)设活塞刚到卡环时温度为T3,此时V3=36S
由于等压变化,有$\frac{V_2}{T_2}=\frac{V_3}{T_3}$
得${T_3}=\frac{V_3}{V_2}{T_2}=\frac{36S}{30S}×300K=360K$
(3)由360K到540K为等容变化
由$\frac{P_3}{T_3}=\frac{P_4}{T_4}$
得 ${P_4}=\frac{T_4}{T_3}P_3^{\;}=\frac{540}{360}×0.8×{10^5}Pa=1.2×{10^5}Pa$
答:(1)活塞与气缸底部之间的距离是30cm;
(2)图(b)中,要使活塞下降到与卡环接触位置则封闭 气体的温度至少为360K;
(3)加热缸中气体到540K时封闭气体的压强为1.2×105Pa.
点评 该题考查几种不同的情况下理想气体的状态方程的应用,正确使用气体状态方程,并根据题目给出的条件求出气体状态参量,根据状态方程求解即可.基础题目.

 通城学典默写能手系列答案
通城学典默写能手系列答案 “假奶粉事件”发生后,国家加强了对奶粉的质量检查.检验奶粉中的碳水化合物(糖)的含量是一个重要指标,可以用“旋光法”来测量糖溶液的浓度,从而鉴定含糖量.偏振光通过糖的水溶液后,偏振方向会相对于传播方向向左或向右旋转一个角度α,这一角度α称为“旋光度”,α的值只与糖溶液的浓度有关,将α的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中正确的是( )
“假奶粉事件”发生后,国家加强了对奶粉的质量检查.检验奶粉中的碳水化合物(糖)的含量是一个重要指标,可以用“旋光法”来测量糖溶液的浓度,从而鉴定含糖量.偏振光通过糖的水溶液后,偏振方向会相对于传播方向向左或向右旋转一个角度α,这一角度α称为“旋光度”,α的值只与糖溶液的浓度有关,将α的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中正确的是( )| A. | 到达O处光的强度不会明显减弱 | |
| B. | 到达O处光的强度会明显减弱 | |
| C. | 将偏振片B转动一个角度,使得O处光强度最大,偏振片B转过的角度小于α | |
| D. | 将偏振片A转动一个角度,使得O处光强度最大,偏振片A转过的角度等于α |
| A. | 所有的能量守恒过程都能自发地发生 | |
| B. | 热传递、摩擦生热和气体自由膨胀都是可逆过程 | |
| C. | 世界上有多种形式的能量如煤、石油、生物能等都来自太阳辐射的能量 | |
| D. | 能的转化过程符合能量守恒定律,因此不会发生能源危机 |
| A. | 哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律 | |
| B. | 开普勒通过研究行星观测记录,发现了行星运动三大定律 | |
| C. | 笛卡尔根据理想斜面实验,提出了力不是维持物体运动的原因 | |
| D. | 牛顿首先将实验事实和逻辑推理(包括数学推演)和谐地结合起来 |
| A. | △p越大,则末动量越大 | B. | △p>0,说明动量增加 | ||
| C. | △p=0,则物体的动量不变 | D. | △p≠0,则物体的动量大小发生变化 |
| A. | 某一物体的动量改变,一定是速度大小改变 | |
| B. | 某一物体的动量改变,一定是速度方向改变 | |
| C. | 某一物体的运动速度改变,其动量可能不变 | |
| D. | 物体的运动状态改变,其动量一定改变 |
 实验桌上有下列实验仪器:
实验桌上有下列实验仪器: 如图所示,左侧是倾角为60°的斜面、右侧是$\frac{1}{4}$圆弧面的物体固定在水平地面上,圆弧面底端切线水平.一根轻绳两端分别系有质量为m1、m2的小球跨过其顶点上的小滑轮.当它们处于平衡状态时,连结m2 小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球视为质点.则两小球的质量之比ml:m2等于2:3;m2小球对圆弧面的压力大小为$\frac{\sqrt{3}}{3}$ m2g.
如图所示,左侧是倾角为60°的斜面、右侧是$\frac{1}{4}$圆弧面的物体固定在水平地面上,圆弧面底端切线水平.一根轻绳两端分别系有质量为m1、m2的小球跨过其顶点上的小滑轮.当它们处于平衡状态时,连结m2 小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球视为质点.则两小球的质量之比ml:m2等于2:3;m2小球对圆弧面的压力大小为$\frac{\sqrt{3}}{3}$ m2g.