题目内容
13. 如图所示,左侧是倾角为60°的斜面、右侧是$\frac{1}{4}$圆弧面的物体固定在水平地面上,圆弧面底端切线水平.一根轻绳两端分别系有质量为m1、m2的小球跨过其顶点上的小滑轮.当它们处于平衡状态时,连结m2 小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球视为质点.则两小球的质量之比ml:m2等于2:3;m2小球对圆弧面的压力大小为$\frac{\sqrt{3}}{3}$ m2g.
如图所示,左侧是倾角为60°的斜面、右侧是$\frac{1}{4}$圆弧面的物体固定在水平地面上,圆弧面底端切线水平.一根轻绳两端分别系有质量为m1、m2的小球跨过其顶点上的小滑轮.当它们处于平衡状态时,连结m2 小球的轻绳与水平线的夹角为600,不计一切摩擦,两小球视为质点.则两小球的质量之比ml:m2等于2:3;m2小球对圆弧面的压力大小为$\frac{\sqrt{3}}{3}$ m2g.
分析 分别以两个小球为研究对象,分析受力情况,由平衡条件求出小球的重力与绳子拉力的关系,再求解两小球的质量之比.对m2小球,由平衡条件求得支持力,再得到m2小球对轨道的压力.
解答  解:先以m1球为研究对象,由平衡条件得知,绳的拉力大小为 T=m1gsin60°…①
解:先以m1球为研究对象,由平衡条件得知,绳的拉力大小为 T=m1gsin60°…①
再以m2球为研究对象,分析受力情况,如图,由平衡条件可知,绳的拉力T与支持力N的合力与重力大小相等、方向相反,作出两个力的合力,由对称性可知,T=N,
2Tcos30°=m2g…②
由①②解得:ml:m2=2:3,N=$\frac{\sqrt{3}}{3}$m2g
由牛顿第三定律知,m2小球对圆弧面的压力大小为$\frac{\sqrt{3}}{3}$m2g.
故答案为:2:3;$\frac{\sqrt{3}}{3}$.
点评 本题采用隔离法研究两个物体的平衡问题,受力分析,作出力图是正确解答的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
3.在平静的水面上,投入一石块,激起频率为5Hz、波长为10cm的水波,假设该水波为理想的横波,经过2s后,水波能将浮在水面上的落叶沿水面方向推动的距离和该波的速度分别为( )
| A. | 0,0.5 m/s | B. | 0.3 m,0.5 m/s | C. | 0.6 m,50 m/s | D. | 1.5 m,50 m/s |
1.关于分子运动,下列说法中正确的是( )
| A. | 布朗运动是液体分子的热运动 | |
| B. | 当分子间的距离变小时,分子力可能减小,也可能增大 | |
| C. | 布朗运动图示中不规则折线表示的就是液体分子的运动轨迹 | |
| D. | 物体温度改变时物体分子的平均动能不一定改变 |
8. 如图所示,两端开口的弯折玻璃管竖直放置,左管有一段高为h1的水银柱,中间一段水银柱h2将管内空气分为两段,右管有一段高为H的水银柱,三段水银柱均静止,则右管内水银柱的高度H为( )
如图所示,两端开口的弯折玻璃管竖直放置,左管有一段高为h1的水银柱,中间一段水银柱h2将管内空气分为两段,右管有一段高为H的水银柱,三段水银柱均静止,则右管内水银柱的高度H为( )
 如图所示,两端开口的弯折玻璃管竖直放置,左管有一段高为h1的水银柱,中间一段水银柱h2将管内空气分为两段,右管有一段高为H的水银柱,三段水银柱均静止,则右管内水银柱的高度H为( )
如图所示,两端开口的弯折玻璃管竖直放置,左管有一段高为h1的水银柱,中间一段水银柱h2将管内空气分为两段,右管有一段高为H的水银柱,三段水银柱均静止,则右管内水银柱的高度H为( )| A. | h1+h2 | B. | h2-h1 | C. | $\frac{{h}_{1}+{h}_{2}}{2}$ | D. | $\frac{{{h_2}-{h_1}}}{2}$ |
5. 如图所示的电路中,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可以视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )
如图所示的电路中,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可以视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )
 如图所示的电路中,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可以视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )
如图所示的电路中,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可以视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )| A. | R1两端的电压将增大 | B. | R2两端的电压将增大 | ||
| C. | 灯泡L将变暗 | D. | 电路的路端电压将增大 |
15. 如图所示,A、B两物体相距s=7m,物体A以vA=4m/s的速度向右匀速运动.而物体B此时的速度vB=10m/s,向右做匀减速运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )
如图所示,A、B两物体相距s=7m,物体A以vA=4m/s的速度向右匀速运动.而物体B此时的速度vB=10m/s,向右做匀减速运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )
 如图所示,A、B两物体相距s=7m,物体A以vA=4m/s的速度向右匀速运动.而物体B此时的速度vB=10m/s,向右做匀减速运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )
如图所示,A、B两物体相距s=7m,物体A以vA=4m/s的速度向右匀速运动.而物体B此时的速度vB=10m/s,向右做匀减速运动,加速度a=-2m/s2.那么物体A追上物体B所用的时间为( )| A. | 7s | B. | 8s | C. | 9s | D. | 10s |
16.学习完高一物理《必修2》后,你认为以下说法正确的是( )
| A. | 借助机械做功可以省力但不可以省功 | |
| B. | 能量守恒定律告诉我们能源是取之不尽用之不竭的 | |
| C. | 机械能可以转化为热能而热能不可以转化为机械能 | |
| D. | 牛顿发现了万有引力定律并测量了万有引力常量 |
 如图所示,矩形线圈abcd与阻值为50Ω的电阻R、理想电流表A组成闭合电路.线圈在有界匀强磁场中绕垂直于磁场的bc边匀速转动,转动的角速度ω=100π rad/s.线圈的匝数N=100,边长ab=0.2m、ad=0.4m,电阻不计.磁场只分布在bc边的左侧,磁感应强度大小B=$\frac{\sqrt{2}}{16π}$T.设线圈平面与中性面重合时开始计时.
如图所示,矩形线圈abcd与阻值为50Ω的电阻R、理想电流表A组成闭合电路.线圈在有界匀强磁场中绕垂直于磁场的bc边匀速转动,转动的角速度ω=100π rad/s.线圈的匝数N=100,边长ab=0.2m、ad=0.4m,电阻不计.磁场只分布在bc边的左侧,磁感应强度大小B=$\frac{\sqrt{2}}{16π}$T.设线圈平面与中性面重合时开始计时.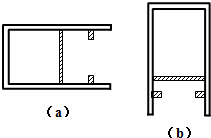 如图(a),一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2.0×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa.现将气缸缓慢转动到开口向下竖直放置,如图(b)所示,取g=10m/s2.求:
如图(a),一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2.0×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,在活塞的右侧12cm处有一对与气缸固定连接的卡环,气体的温度为300K,大气压强P0=1.0×105Pa.现将气缸缓慢转动到开口向下竖直放置,如图(b)所示,取g=10m/s2.求: