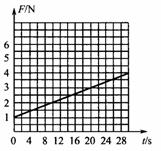
题目内容
(20分)如图所示,接地的空心导体球壳内半径为R,在空腔内一直径上的P1和P2处,放置电量分别为q1和q2的点电荷,q1=q2=q,两点电荷到球心的距离均为a.由静电感应与静电屏蔽可知:导体空腔内表面将出现感应电荷分布,感应电荷电量等于-2q.空腔内部的电场是由q1、q2和两者在空腔内表面上的感应电荷共同产生的.由于我们尚不知道这些感应电荷是怎样分布的,所以很难用场强叠加原理直接求得腔内的电势或场强.但理论上可以证明,感应电荷对腔内电场的贡献,可用假想的位于腔外的(等效)点电荷来代替(在本题中假想(等效)点电荷应为两个),只要假想的(等效)点电荷的位置和电量能满足这样的条件,即:设想将整个导体壳去掉,由q1在原空腔内表面的感应电荷的假想(等效)点电荷![]() 与q1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q2在原空腔内表面的感应电荷的假想(等效)点电荷
与q1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q2在原空腔内表面的感应电荷的假想(等效)点电荷![]() 与q2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷
与q2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷![]() 、
、![]() 和q1、q2来计算原来导体存在时空腔内部任意点的电势或场强.
和q1、q2来计算原来导体存在时空腔内部任意点的电势或场强.
1.试根据上述条件,确定假想等效电荷![]() 、
、![]() 的位置及电量.
的位置及电量.
2.求空腔内部任意点A的电势UA.已知A点到球心O的距离为r,![]() 与
与![]() 的夹角为θ .
的夹角为θ .
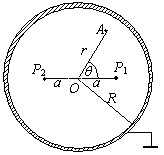
1.解法Ⅰ:
如图1所示,
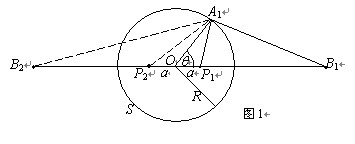
S为原空腔内表面所在位置,![]() 的位置应位于
的位置应位于![]() 的延长线上的某点B1处,
的延长线上的某点B1处,![]() 的位置应位于
的位置应位于![]() 的延长线上的某点B2处.设A1为S面上的任意一点,根据题意有
的延长线上的某点B2处.设A1为S面上的任意一点,根据题意有
![]() (1)
(1)
![]() (2)
(2)
怎样才能使 (1) 式成立呢?下面分析图1中![]() 与
与![]() 的关系.
的关系.
若等效电荷![]() 的位置B1使下式成立,即
的位置B1使下式成立,即
![]() (3)
(3)
即 ![]() (4)
(4)
则 ![]()
有 ![]() (5)
(5)
由 (1)式和 (5)式便可求得等效电荷![]()
![]() (6)
(6)
由 (3) 式知,等效电荷![]() 的位置B1到原球壳中心位置O的距离
的位置B1到原球壳中心位置O的距离
![]() (7)
(7)
同理,B2的位置应使![]() ,用类似的方法可求得等效电荷
,用类似的方法可求得等效电荷
![]() (8)
(8)
等效电荷![]() 的位置B2到原球壳中心O位置的距离
的位置B2到原球壳中心O位置的距离
![]() (9)
(9)
解法Ⅱ:
在图1中,设![]() ,
,![]() ,
,![]() .根据题意,
.根据题意,![]() 和
和![]() 两者在A1点产生的电势和为零.有
两者在A1点产生的电势和为零.有
![]() (1')
(1')
式中
![]() (2')
(2')
![]() (3')
(3')
由(1')、(2')、(3')式得
![]() (4')
(4')
(4')式是以![]() 为变量的一次多项式,要使(4')式对任意
为变量的一次多项式,要使(4')式对任意![]() 均成立,等号两边的相应系数应相等,即
均成立,等号两边的相应系数应相等,即
![]() (5')
(5')
![]() (6')
(6')
由(5')、(6')式得
![]() (7')
(7')
解得 ![]() (8')
(8')
由于等效电荷位于空腔外部,由(8')式求得
![]() (9')
(9')
由(6')、(9')式有
![]() (10')
(10')
考虑到(1')式,有
![]() (11')
(11')
同理可求得
![]() (12')
(12')
![]() (13')
(13')
2.A点的位置如图2所示.
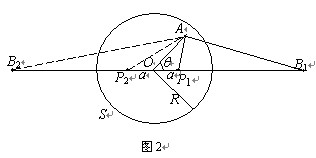
A的电势由q1、![]() 、q2、
、q2、![]() 共同产生,即
共同产生,即
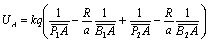 (10)
(10)
因
![]()
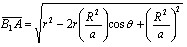
![]()
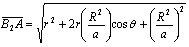
代入 (10) 式得
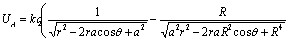
![]()
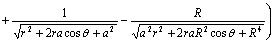 (11)
(11)
评分标准:
本题20分.第1问18分,解法Ⅰ中(1)、(2)、(6)、(7)、(8)、(9) 式各3分.解法Ⅱ的评分可参考解法Ⅰ.
第2问2分,即(11)式2分.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案


 和
和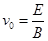 :将显微镜置于C点,控制粒子源,使其只向K点发射粒子。电场与磁场共存一段时间t1后再撤去磁场,又经时间t2后,粒子到达显微镜。求两段时间的比值t1∶t2。
:将显微镜置于C点,控制粒子源,使其只向K点发射粒子。电场与磁场共存一段时间t1后再撤去磁场,又经时间t2后,粒子到达显微镜。求两段时间的比值t1∶t2。