题目内容
带电粒子以速度v垂直于磁场方向进入磁感应强度为B的匀强磁场,做半径为r的匀速圆周运动.
(1)求该带电粒子的比荷.
(2)其他条件不变,速度增大为2v,半径和周期是否变化?说明理由.
(1)求该带电粒子的比荷.
(2)其他条件不变,速度增大为2v,半径和周期是否变化?说明理由.
分析:(1)带电粒子在垂直于磁场的方向做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律和向心力公式列式求解荷质比.
(2)由上题得到半径公式,由圆周运动的规律推导出周期表达式,再进行分析.
(2)由上题得到半径公式,由圆周运动的规律推导出周期表达式,再进行分析.
解答:解:(1)带电粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律得:
qvB=m
则得:
=
(2)由qvB=m
得:r=
,可知r∝v,速度增大为2v,半径增大为2r;
周期 T=
=
,可知T与v无关,所以速度增大为2v时,周期不变.
答:(1)该带电粒子的比荷是
.(2)其他条件不变,速度增大为2v,半径增大为2r,周期不变.
qvB=m
| v2 |
| r |
则得:
| q |
| m |
| v |
| rB |
(2)由qvB=m
| v2 |
| r |
| mv |
| qB |
周期 T=
| 2πr |
| v |
| 2πm |
| qB |
答:(1)该带电粒子的比荷是
| v |
| rB |
点评:对于磁场中圆周运动动力学问题,关键分析受力情况,根据洛伦兹力提供向心力,求解半径和周期.

练习册系列答案
相关题目
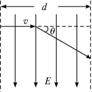
 如图所示,电荷量为q,质量为m的带电粒子以速度v垂直进入平行板电容器中(不计粒子的重力),已知极板的长度为l,两极板间的距离为d,两极板间的电压为U,试推导带电粒子射出电容器时在偏转电场中的偏转位移y和偏转角Φ的表达式.
如图所示,电荷量为q,质量为m的带电粒子以速度v垂直进入平行板电容器中(不计粒子的重力),已知极板的长度为l,两极板间的距离为d,两极板间的电压为U,试推导带电粒子射出电容器时在偏转电场中的偏转位移y和偏转角Φ的表达式.