题目内容
19. 图甲所示的平行板电容器板间距离为d,两板所加电压随时间变化图线如图乙所示,t=0时刻,质量为m、带电量为q的粒子以平行于极板的速度V0射入电容器,t1=3T时刻恰好从下极板边缘射出电容器,带电粒子的重力不计,求:
图甲所示的平行板电容器板间距离为d,两板所加电压随时间变化图线如图乙所示,t=0时刻,质量为m、带电量为q的粒子以平行于极板的速度V0射入电容器,t1=3T时刻恰好从下极板边缘射出电容器,带电粒子的重力不计,求:(1)平行板电容器板长L
(2)粒子射出电容器时偏转的角度φ
(3)粒子射出电容器时竖直偏转的位移y.
分析 (1)带电粒子在电场中受电场力作用做匀加速直线运动,在垂直电场方向粒子做匀速直线运动,根据运动的合成与分解求解板长L;
(2)根据电压随时间变化的图象知,在T-2T时间内板间无电场,粒子不受力做匀速直线运动,根据运动的合成与分解求解粒子在电场中偏转的倾角;
(3)同样根据有电场时粒子在竖直方向做匀加速直线运动,没有电场时在竖直方向做匀速运动,分三段考虑粒子偏转的位移.
解答 解:(1)带电粒子在电场中运动的时间t=3T,由题意知,带电粒子在电场方向上做匀变速运动,在垂直电场方向上不受力做匀速直线运动,所以有:
平行板电容器极板长度L=v0t=3v0T
(2)粒子在电容器中运动时,在电场方向做匀加速运动,在垂直电场方向做匀速直线运动,根据电场图象可知:
在0-T的时间里,粒子在电场方向(垂直板的方向)做匀加速运动,加速度a=$\frac{qU}{md}$,初速度为0,末速度为aT
在T-2T时间里,粒子不受电场力作用(垂直板的方向)粒子做速度v=aT的匀速直线运动
在2T-3T时间里,粒子在电场方向做初速度v=aT的匀加速直线运动,加速度a=$\frac{qU}{md}$
则末速度为2aT
所以粒子在垂直板的方向即y方向的末速度为vy=2aT=2$\frac{qU}{md}$T
粒子在平行板的方向即x方向的末速度vx=v0
射出电容器时,偏转角度为φ,则tanφ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{2qUT}{md{v}_{0}}$
故φ=arctan$\frac{2qUT}{md{v}_{0}}$
(3)由(2)分析知,粒子在0~T,垂直板的方向做初速度为0的匀加速直线运动,加速度a=$\frac{qU}{md}$,时间t=T,所以在y方向偏转的位移y1=$\frac{1}{2}a{t}_{1}^{2}$=$\frac{1}{2}×\frac{U}{d}×\frac{q}{m}$•T2
T~2T,垂直板的方向做初速度v=aT的匀速直线运动,则在y方向偏转的位移y2=vT=(aT)T=$\frac{qU}{md}$T2;
2T~3T,垂直板的方向做初速度v=aT,加速度a=$\frac{qU}{md}$的匀加速直线运动,
故在y方向偏转的位y3=vT+$\frac{1}{2}$aT2=(aT)T+$\frac{1}{2}$aT2=$\frac{3}{2}$$\frac{qU}{md}$T2
所以在粒子射出电场的3T时间内竖直方向偏转的位移y=y1+y2+y3=$\frac{3qU{T}^{2}}{md}$
答:(1)平行板电容器板长为3v0T;
(2)粒子从射入到射出电容器时速度偏转的角度φ为arctan$\frac{2qUT}{md{v}_{0}}$;
(3)粒子从射入到射出电容器时竖直方向偏转的位移y为$\frac{3qU{T}^{2}}{md}$.
点评 根据运动的合成与分解,分析粒子在竖直方向多过程的位移和速度,是解决本题的关键.

 2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )
2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )| A. | 若存在磁铁矿,则指示灯不亮;调节电阻R的大小,对该探测仪的灵敏度无影响 | |
| B. | 若存在磁铁矿,则指示灯不亮;调节电阻R的大小,对该探测仪的灵敏度有影响 | |
| C. | 若存在磁铁矿,则指示灯亮;调节电阻R的大小,对该探测仪的灵敏度无影响 | |
| D. | 若存在磁铁矿,则指示灯亮;调节电阻R的大小,对该探测仪的灵敏度有影响 |
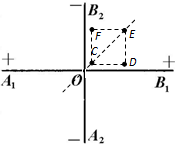 理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场.现有两块无限大的均匀绝缘带电平板,正交放置如图所示,A1B1两面正电,A2B2两面负电,且单位面积所带电荷量相等(设电荷不发生移动).图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、E、F恰好位于纸面内正方形的四个顶点上,且CE的连线过O点.则下列说法中正确的是( )
理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场.现有两块无限大的均匀绝缘带电平板,正交放置如图所示,A1B1两面正电,A2B2两面负电,且单位面积所带电荷量相等(设电荷不发生移动).图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、E、F恰好位于纸面内正方形的四个顶点上,且CE的连线过O点.则下列说法中正确的是( )| A. | C、E两点场强相同 | |
| B. | D、F两点电势相同 | |
| C. | 电子从C点移到D点电场力做正功 | |
| D. | 在C、D、E、F四个点中电子在F点具有的电势能最大 |
 P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )
P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )| A. | Q带正电荷 | |
| B. | c点的电势高于d点电势 | |
| C. | b点的电场强度大于a点的电场强度 | |
| D. | 在带电粒子从a点运动到b点的过程中,电场力做负功 |
| A. | 平抛运动是非匀变速曲线运动 | |
| B. | 匀速圆周运动的线速度、角速度、周期都是不变的 | |
| C. | 牛顿第三定律在物体处于非平衡状态时也一样适用 | |
| D. | 物体沿光滑斜面下滑,由于惯性物体的速度不断增大 |

 如图所示,封闭有一定质量理想气体的气缸开口向下竖直放置,活塞的截面积为S,质量为m0,活塞通过轻绳连接了一个质量为m的重物.若开始时气缸内理想气体的温度为T0,轻绳刚好伸直且对活塞无拉力作用,外界大气压强为P0,一切摩擦均不计.
如图所示,封闭有一定质量理想气体的气缸开口向下竖直放置,活塞的截面积为S,质量为m0,活塞通过轻绳连接了一个质量为m的重物.若开始时气缸内理想气体的温度为T0,轻绳刚好伸直且对活塞无拉力作用,外界大气压强为P0,一切摩擦均不计.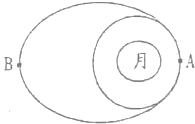 “嫦娥一号”的成功发射,为实现中华民族几千年的本月梦想迈出了重要的一步,如图所示,“嫦娥一号”先进入绕月飞行的椭圆轨道,然后在椭圆轨道近月点A变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点B距月球表面高度为H;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为h,飞行周期为T,月球的半径为R,万有引力常量为G;再然后,假设宇航长在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为r的圆周运动,宇航员质量是m,飞船经过最低点时的速度是v,求:
“嫦娥一号”的成功发射,为实现中华民族几千年的本月梦想迈出了重要的一步,如图所示,“嫦娥一号”先进入绕月飞行的椭圆轨道,然后在椭圆轨道近月点A变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点B距月球表面高度为H;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为h,飞行周期为T,月球的半径为R,万有引力常量为G;再然后,假设宇航长在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为r的圆周运动,宇航员质量是m,飞船经过最低点时的速度是v,求: