题目内容
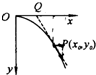
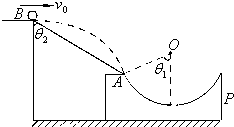
如图所示,P是水平面上的圆弧凹槽.从高台边B点以某速度v0水平飞出的小球(可看做质点),恰能从固定在某位置的凹槽的圆弧轨道的左端A点沿圆弧切线方向进入轨道.O是圆弧的圆心,θ1是OA与竖直方向的夹角,θ2是BA与竖直方向的夹角.若tanθ2=
,则( )
2
| ||
| 3 |
| A.θ1=60° | B.θ1=45° | C.θ1=30° | D.θ1=53° |

平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.
由题意:小球从A点沿圆弧切线方向进入轨道,经过A点的速度沿圆弧A点的切线方向,则根据速度的分解可得:速度与水平方向的夹角为θ1,则:
tanθ1=
.
对于平抛运动,位移与竖直方向的夹角为θ2,则tanθ2=
=
=
联立得:tanθ1=
据题有:tanθ2=
联立解得:θ1=60°
故选:A
由题意:小球从A点沿圆弧切线方向进入轨道,经过A点的速度沿圆弧A点的切线方向,则根据速度的分解可得:速度与水平方向的夹角为θ1,则:
tanθ1=
| vy |
| v0 |
对于平抛运动,位移与竖直方向的夹角为θ2,则tanθ2=
| x |
| y |
| v0t | ||
|
| 2v0 |
| vy |
联立得:tanθ1=
| 2 |
| tanθ2 |
据题有:tanθ2=
2
| ||
| 3 |
联立解得:θ1=60°
故选:A

练习册系列答案
相关题目