题目内容
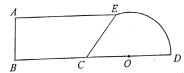
【题目】如图所示为轮滑比赛的一段模拟赛道。一个小物块从A点以一定的初速度水平抛出，刚好无碰撞地从C点进入光滑的圆弧赛道，圆弧赛道所对的圆心角为60°，圆弧半径为R，圆弧赛道的最低点与水平赛道DE平滑连接，DE长为R，物块经圆弧赛道进入水平赛道，然后在E点无碰撞地滑上左侧的斜坡，斜坡的倾角为37°，斜坡也是光滑的，物块恰好能滑到斜坡的最高点F，F、O、A三点在同一高度，重力加速度大小为g，不计空气阻力，不计物块的大小。求：
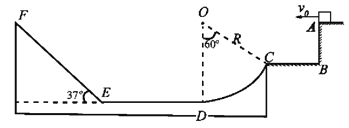
(1)物块的初速度v0大小及物块与水平赛道间的动摩擦因数；
(2)试判断物块向右返回时，能不能滑到C点，如果能，试分析物块从C点抛出后，会不会直接撞在竖直墙AB上；如果不能，试分析物块最终停在什么位置?
【答案】(1) 
, 
(2)物块刚好落在平台上的B点
【解析】
（1）小物块从A点以一定的初速度水平抛出，刚好无碰撞地从C点进入光滑的圆弧赛道，根据水平速度不变求解C点的速度；根据机械能守恒定律列式可求解小球的初速度v0；物块从A到F的过程，根据动能定理列式可求解物块与水平赛道间的动摩擦因数；
（2）假设物块向右返回时，能滑到C点，根据动能定理列式求解C点的速度，若有解说明假设正确；结合平抛运动的规律求解物块最终停在什么位置.
（1）物块从A点抛出后做平抛运动，在C点的速度大小为
几何关系可知AB的高度：h=Rcos600=0.5R；
设物块的质量为m，从A到B点的过程，根据机械能守恒定律：
解得
物块从A到F的过程，根据动能定理：
解得
（2）假设物块能回到C点，设到达C点的速度大小为vC′，根据动能定理：
求得
假设成立；
假设物块从C点抛出后直接落在BC平台上，BC长度：
物块在C点竖直方向的分速度
水平分速度：
落在BC平台上的水平位移：
即物块刚好落在平台上的B点.
