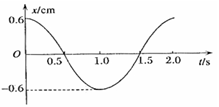
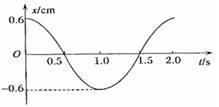
题目内容
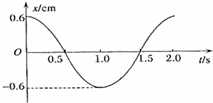 一弹簧振子小球的质量为m=0.5kg,弹簧的劲度系数k=4.9N/m,振子在光滑水平面内做简谐运动的图象如下图所示,则小球具有正向最大加速度的时刻为
一弹簧振子小球的质量为m=0.5kg,弹簧的劲度系数k=4.9N/m,振子在光滑水平面内做简谐运动的图象如下图所示,则小球具有正向最大加速度的时刻为1.0
1.0
s,其最大值为0.06
0.06
m/s2,在t=1.75s时,小球加速度为0.04
0.04
m/s2,方向为-x方向
-x方向
.分析:根据简谐运动的特点:加速度大小与位移大小成正比,方向与位移方向相反,当位移为负向最大时,加速度为正向最大.根据振动方程求出振子t=1.75s的位移,由牛顿第二定律求出加速度的大小和方向.
解答:解:根据简谐运动的特点a=-
,当位移为负向最大时,加速度为正向最大,则小球具有正向最大加速度的时刻为1.0s,最大加速度am=-
=
≈0.06m/s2.由图读出周期为T=2s,ω=
=πrad/s,则振动方程为x=Acosωt=0.6cosπt(cm),当t=1.75s,x=0.6cosπ×1.75cm≈0.4cm,加速度a=-
≈-0.04m/s2,方向为-x方向.
故答案为:1.0,0.06,0.04,-x方向
| kx |
| m |
| kx |
| m |
| 4.9×0.6×10-2 |
| 0.5 |
| 2π |
| T |
| kx |
| m |
故答案为:1.0,0.06,0.04,-x方向
点评:本题关键要抓住简谐运动的特征方程:a=-
.对于任意时刻的位移,可根据振动方程求解.
| kx |
| m |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
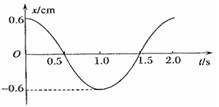 一弹簧振子小球的质量为m=0.5kg,弹簧的劲度系数k=4.9N/m,振子在光滑水平面内做简谐运动的图象如下图所示,则小球具有正向最大加速度的时刻为___s,其最大值为___m/s2,在t=1.75s时,小球加速度为_____m/s2,方向为___。
一弹簧振子小球的质量为m=0.5kg,弹簧的劲度系数k=4.9N/m,振子在光滑水平面内做简谐运动的图象如下图所示,则小球具有正向最大加速度的时刻为___s,其最大值为___m/s2,在t=1.75s时,小球加速度为_____m/s2,方向为___。