题目内容
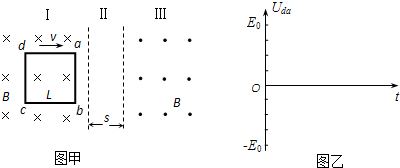
如图甲所示,空间有Ⅰ区和Ⅲ区两个有理想边界的匀强磁场区域,磁感应强度大小均为B,方向如图所示.两磁场区域之间有宽度为s的无磁场区域Ⅱ.abcd是由均匀电阻丝做成的边长为L(L>s)的正方形线框,每边的电阻为R.线框以垂直磁场边界的速度v水平向右匀速运动,从Ⅰ区经过Ⅱ区完全进入Ⅲ区,线框ab边始终与磁场边界平行.求:
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小和方向;
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热;
(3)请在图乙的坐标图中画出,从ab边刚进入Ⅱ区,到cd边刚进入Ⅲ区的过程中,
d、a两点间的电势差Uda随时间t变化的图线.其中E0=BLv.
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小和方向;
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热;
(3)请在图乙的坐标图中画出,从ab边刚进入Ⅱ区,到cd边刚进入Ⅲ区的过程中,
d、a两点间的电势差Uda随时间t变化的图线.其中E0=BLv.

分析:(1)当ab边在Ⅱ区运动时,dc边切割磁感线产生感应电动势,由E=BLv、I=
、F=BIL结合求出安培力的大小,由左手定则判断安培力的方向.
(2)分段求出线框中感应电流和运动时间,由焦耳定律求焦耳热,再得到总热量.
(3)分段求出d、a两点间的电势差,再画出图象.
| E |
| 4R |
(2)分段求出线框中感应电流和运动时间,由焦耳定律求焦耳热,再得到总热量.
(3)分段求出d、a两点间的电势差,再画出图象.
解答:解:(1)dc边产生的感应电动势 E=BLv 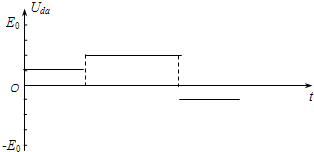
线框中的感应电流 I=
dc边所受的安培力 F=BIL
求得F=
,方向水平向左
(2)ab边经过Ⅱ区时,设电流为I1,所用时间为t1,产生的热为Q1
有 I1=
,t1=
由焦耳定律 Q1=I1 2?4Rt1,Uda=
BLv
从ab边进入Ⅲ区到cd边进入Ⅱ区,设电流为I2,所用时间为t2,产生的热为Q2,则有
I2=
,t2=
由焦耳定律得 Q2=I2 2?4Rt2,Uda=-
×2BLv=
BLv
整个过程中产生的热 Q=2Q1+Q2
解得,Q=
从cd边进入Ⅱ区到cd边进入Ⅲ区,Uda=-
BLv
(3)
画出d、a两点间的电势差Uda随时间t变化的图线如图.
答:
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小为
,方向水平向左;
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热是
;
(3)图象如图所示.

线框中的感应电流 I=
| E |
| 4R |
dc边所受的安培力 F=BIL
求得F=
| B2L2v |
| 4R |
(2)ab边经过Ⅱ区时,设电流为I1,所用时间为t1,产生的热为Q1
有 I1=
| E |
| 4R |
| s |
| v |
由焦耳定律 Q1=I1 2?4Rt1,Uda=
| 1 |
| 4 |
从ab边进入Ⅲ区到cd边进入Ⅱ区,设电流为I2,所用时间为t2,产生的热为Q2,则有
I2=
| 2E |
| 4R |
| L-s |
| v |
由焦耳定律得 Q2=I2 2?4Rt2,Uda=-
| 1 |
| 4 |
| 1 |
| 2 |
整个过程中产生的热 Q=2Q1+Q2
解得,Q=
| B2L2v(2L-s) |
| 2R |
从cd边进入Ⅱ区到cd边进入Ⅲ区,Uda=-
| 1 |
| 4 |
(3)
画出d、a两点间的电势差Uda随时间t变化的图线如图.
答:
(1)当ab边在Ⅱ区运动时,dc边所受安培力的大小为
| B2L2v |
| 4R |
(2)线框从完全在Ⅰ区开始到全部进入Ⅲ区的整个运动过程中产生的焦耳热是
| B2L2v(2L-s) |
| 2R |
(3)图象如图所示.
点评:本题是电磁感应与电路知识的综合,掌握法拉第电磁感应定律、欧姆定律和焦耳定律,学会分过程研究是基本能力.

练习册系列答案
相关题目
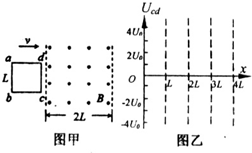 如图甲所示.空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面外,abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度υ匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.求:
如图甲所示.空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面外,abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度υ匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.求: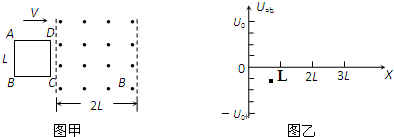
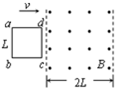 如图甲所示,空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.则ab两端电势差Uab随距离变化的图象正确的是(其中U0=BLv)( )
如图甲所示,空间有一宽为2L的匀强磁场区域,磁感应强度为B,方向垂直纸面向外.abcd是由均匀电阻丝做成的边长为L的正方形线框,总电阻为R.线框以垂直磁场边界的速度v匀速通过磁场区域.在运动过程中,线框ab、cd两边始终与磁场边界平行.设线框刚进入磁场的位置x=0,x轴沿水平方向向右.则ab两端电势差Uab随距离变化的图象正确的是(其中U0=BLv)( )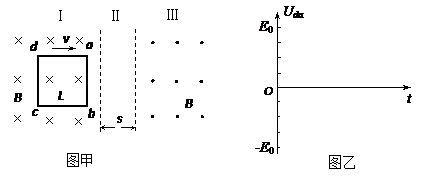 d、a两点间的电势差Uda随时间t变化的图线。其中E0 = BLv 。
d、a两点间的电势差Uda随时间t变化的图线。其中E0 = BLv 。