题目内容
16.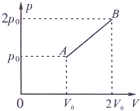 1mol理想气体的压强p与体积V关系如图所示.气体在状态A时的压强为p0、体积为V0,热力学温度为T0,在状态B时的压强为2p0,体积为2V0,AB为直线段.已知该气体内能与温度成正比U=CvT( Cv为比例系数).求:
1mol理想气体的压强p与体积V关系如图所示.气体在状态A时的压强为p0、体积为V0,热力学温度为T0,在状态B时的压强为2p0,体积为2V0,AB为直线段.已知该气体内能与温度成正比U=CvT( Cv为比例系数).求:①气体在B状态时的热力学温度;
②气体从状态A变化到状态B的过程中,吸收的热量.
分析 ①由A到B过程根据理想气体状态方程列式求解;
②根据热力学第一定律列式求解.
解答 解:①由题意得:状态A:PA=P0 VA=V0 TA=T0
状态B:PB=2P0 VB=2V0
根据理想气体状态方程得:$\frac{{P}_{A}{V}_{A}}{{T}_{A}}=\frac{{P}_{B}{V}_{B}}{{T}_{B}}$
代入数据解得:TB=4T0
②在P-V图象中面积表示做的功,由A到B过程体积增大,气体对外做功为:
$W=\frac{{(P}_{0}+2{P}_{0})(2{V}_{0}-{V}_{0})}{2}=\frac{3{P}_{0}{V}_{0}}{3}$
气体内能与温度成正比U=CvT
所以△U=CV4T0-CVT0=3CVT0
根据热力学第一定律得:△U=-W+Q,
以上各式联立解得:$Q=W+△U=3{C}_{V}{T}_{0}+\frac{3{P}_{0}{V}_{0}}{2}$
答:①气体在B状态时的热力学温度为4T0;
②气体从状态A变化到状态B的过程中,吸收的热量为$3{C}_{V}{T}_{0}+\frac{3{P}_{0}{V}_{0}}{2}$.
点评 本题考察理想气体的状态方程和热力学第一定律,特别注意在P-V图象中面积表示气体对外界或外界对气体做的功,体积增大为负,体积减小为正.

练习册系列答案
相关题目
6.某实验小组用伏安法测量一段金属丝的电阻Rx,实验所用器材为:电池组(电动势3V,内阻约为1Ω)、电流表(内阻约0.1Ω)、电压表(内阻约3KΩ)、滑动变阻器R(0~20Ω,额定电流2A)、开关、导线若干.
(1)该小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
由以上实验数据可知,他们测量Rx是采用下面图中的乙 图(选填“甲”或“乙”).
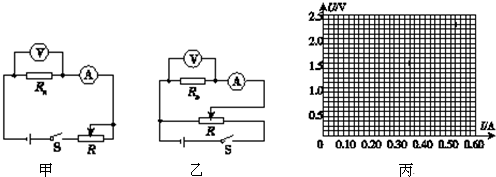
(2)该小组的同学在坐标纸上建立U-I坐标系,如图丙所示,图中已标出了与测量数据对应的4个坐标点.请在图中标出第2、4、6次测量数据的坐标点,并描绘出U-I图线.由图线得出金属丝的电阻值Rx=4.4Ω(保留两位有效数字).
(3)任何实验测量都存在误差.本实验所用测量仪器均已校准,下列关于本实验中误差的说法中正确的选项是B.
A.由于电流表和电压表内阻引起的误差属于偶然误差
B.用U-I图象处理数据来求金属丝的电阻可以减少偶然误差.
C.由于读数引起的误差属于系统误差
D.若将电流表和电压表的内阻计算在内,可以消除由测量仪表引起的偶然误差.
(1)该小组同学利用以上器材正确连接好电路,进行实验测量,记录数据如下:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.10 | 0.30 | 0.70 | 1.00 | 1.50 | 1.70 | 2.30 |
| I/A | 0.020 | 0.060 | 0.160 | 0.220 | 0.340 | 0.460 | 0.520 |

(2)该小组的同学在坐标纸上建立U-I坐标系,如图丙所示,图中已标出了与测量数据对应的4个坐标点.请在图中标出第2、4、6次测量数据的坐标点,并描绘出U-I图线.由图线得出金属丝的电阻值Rx=4.4Ω(保留两位有效数字).
(3)任何实验测量都存在误差.本实验所用测量仪器均已校准,下列关于本实验中误差的说法中正确的选项是B.
A.由于电流表和电压表内阻引起的误差属于偶然误差
B.用U-I图象处理数据来求金属丝的电阻可以减少偶然误差.
C.由于读数引起的误差属于系统误差
D.若将电流表和电压表的内阻计算在内,可以消除由测量仪表引起的偶然误差.
7.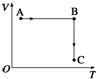 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )| A. | 在过程AB中,气体压强不断变大 | B. | 在过程BC中,气体密度不断变大 | ||
| C. | 在过程AB中,气体对外界做功 | D. | 在过程BC中,外界对气体做功 |
1.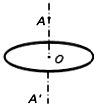 如图所示,一均匀带正电绝缘细圆环水平固定,环心为O点.带正电的小球从O点正上方的A点由静止释放,穿过圆环中心O,并通过关于O与A点对称的A′点,取O点为重力势能零点.关于小球从A点运动到A′点的过程中,小球的加速度a、重力势能EpG、机械能E、电势能EpE随位置变化的情况,下列说法中正确的是( )
如图所示,一均匀带正电绝缘细圆环水平固定,环心为O点.带正电的小球从O点正上方的A点由静止释放,穿过圆环中心O,并通过关于O与A点对称的A′点,取O点为重力势能零点.关于小球从A点运动到A′点的过程中,小球的加速度a、重力势能EpG、机械能E、电势能EpE随位置变化的情况,下列说法中正确的是( )
 如图所示,一均匀带正电绝缘细圆环水平固定,环心为O点.带正电的小球从O点正上方的A点由静止释放,穿过圆环中心O,并通过关于O与A点对称的A′点,取O点为重力势能零点.关于小球从A点运动到A′点的过程中,小球的加速度a、重力势能EpG、机械能E、电势能EpE随位置变化的情况,下列说法中正确的是( )
如图所示,一均匀带正电绝缘细圆环水平固定,环心为O点.带正电的小球从O点正上方的A点由静止释放,穿过圆环中心O,并通过关于O与A点对称的A′点,取O点为重力势能零点.关于小球从A点运动到A′点的过程中,小球的加速度a、重力势能EpG、机械能E、电势能EpE随位置变化的情况,下列说法中正确的是( )| A. | 从A到O的过程中a一定先增大后减小,从O到A′的过程中a一定先减小后增大 | |
| B. | 从A到O的过程中EpG小于零,从O到A′的过程中EpG大于零 | |
| C. | 从A到O的过程中E随位移增大均匀减小,从O到A′的过程中E随位移增大均匀增大 | |
| D. | 从A到O的过程中EpE随位移增大非均匀增大,从O到A′的过程中EpE随位移增大非均匀减小 |
8.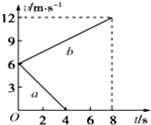 质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
 质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )| A. | 1:2 | B. | 2:1 | C. | 3:1 | D. | 3:2 |
5.下列说法正确的是( )
| A. | 已知阿伏加德罗常数、气体摩尔质量和密度,可算出该气体分子间的平均距离 | |
| B. | 布朗运动是指悬浮在液体中的固体颗粒的无规则运动 | |
| C. | 给自行车轮胎打气时,打到后面很难打,是因为气体分子间存在斥力的缘固 | |
| D. | 物质是晶体还是非晶体,比较可靠的办法是从各向异性或各向同性来判断 | |
| E. | 热力学第二定律也叫做熵增加原理 |
6.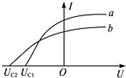 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | a光的频率更大 | |
| B. | 在增大电压U时,光电流一定都会增大 | |
| C. | 照射该光电管时a光单位时间发生的光电子数多 | |
| D. | 照射该光电管时b光使其逸出的光电子最大初动能大 |
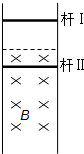 如图所示,竖直平面内固定间距为L=0.5m的光滑金属导轨(电阻不计),虚线下方存在垂直于导轨平面的匀强磁场,磁感应强度B=1T.两根质量相同、电阻均为R=1Ω的完全相同金属杆水平放置在导轨上,与导轨接触良好.在磁场外固定杆Ⅰ,在磁场内静止释放杆Ⅱ,经过一段时间后开始匀速运动,速度v=4m/s.求:
如图所示,竖直平面内固定间距为L=0.5m的光滑金属导轨(电阻不计),虚线下方存在垂直于导轨平面的匀强磁场,磁感应强度B=1T.两根质量相同、电阻均为R=1Ω的完全相同金属杆水平放置在导轨上,与导轨接触良好.在磁场外固定杆Ⅰ,在磁场内静止释放杆Ⅱ,经过一段时间后开始匀速运动,速度v=4m/s.求: