题目内容
11.某同学用如图甲所示的实验器材测定重力加速度.实验器材有:小钢珠、固定底 座、带有标尺的竖直杆、光电门1和2组成的光电计时器,小钢珠释放器(可使小钢珠无初速释放)、网兜.实验时改变光电门1的位置,保持光电门2的位置不变,用光电计时器记录小钢珠从光电门1运动至光电门2的时间t,并从竖直杆上读出两光电门间的距离h.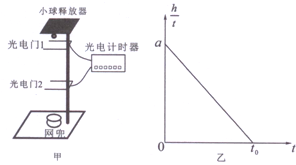
(1)设小钢珠经过光电门2的速度为v,当地的重力加速度为g,不考虑空气阻力,则h、t、g、v四个物理量之间的关系为h=vt-$\frac{1}{2}$gt2;
(2)多次测量并记录h、t,根据实验数据作出 $\frac{h}{t}$-t图象,如图乙所示(纵、横轴截距为a,t0),根据图线可求出重力加速度大小为$\frac{2a}{{t}_{0}}$,小钢珠通过光电门2时的速度为a.
分析 根据自由下落的公式和匀变速直线运动的推论求出h、t、g、v四个物理量之间的关系.
整理得到$\frac{h}{t}$-t图线的表达式,并找出图线的斜率和加速度关系.
解答 解:(1)小球经过光电门2的速度为v,根据运动学公式得从开始释放到经过光电门2的时间t′=$\frac{v}{g}$,
所以从开始释放到经过光电门1的时间t″=t′-t=$\frac{v}{g}$-t,
所以经过光电门1的速度v′=gt″=v-gt;
根据匀变速直线运动的推论得:两光电门间的距离h=$\frac{v′+v}{2}$t=vt-$\frac{1}{2}$gt2.
(2)根据h=vt-$\frac{1}{2}$gt2
得,$\frac{h}{t}$=v-$\frac{1}{2}$gt,
则 $\frac{h}{t}$-t图线斜率的绝对值为k,k=$\frac{1}{2}$g,
所以重力加速度大小g=2$\frac{a}{{t}_{0}}$=$\frac{2a}{{t}_{0}}$.
因此图象的纵截距即为小钢珠通过光电门2时的速度a;
故答案为:(1)vt-$\frac{1}{2}$gt2; (2)$\frac{2a}{{t}_{0}}$,a.
点评 解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,本题的第一问,也可以采用逆向思维,结合位移时间公式进行求解.

练习册系列答案
相关题目
1.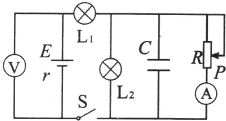 在如图所示的电路中,电压表和电流表均为理想电表,电源内阻不能忽略,闭合开关S后,将滑动变阻器的滑片P向下调节,则下列叙述正确的是( )
在如图所示的电路中,电压表和电流表均为理想电表,电源内阻不能忽略,闭合开关S后,将滑动变阻器的滑片P向下调节,则下列叙述正确的是( )
 在如图所示的电路中,电压表和电流表均为理想电表,电源内阻不能忽略,闭合开关S后,将滑动变阻器的滑片P向下调节,则下列叙述正确的是( )
在如图所示的电路中,电压表和电流表均为理想电表,电源内阻不能忽略,闭合开关S后,将滑动变阻器的滑片P向下调节,则下列叙述正确的是( )| A. | 电压表和电流表的示数都增大 | B. | 灯L2变暗,电流表的示数减小 | ||
| C. | 灯L1变暗,电压表的示数增大 | D. | 电容器C所带电荷量减小 |
2.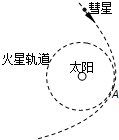 据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
 据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )| A. | 可计算出彗星的质量 | |
| B. | 可计算出彗星经过A点时受到的引力 | |
| C. | 可计算出彗星经过A点的速度大小 | |
| D. | 可确定彗星在A点的速度大于火星绕太阳的速度 |
19. 春节许多广场都有飞镖、空桶、套圈等项目.某同学在玩飞镖时,距地面高h、离靶面距离L处,将质量为m的飞镖以速度v0水平投出,落在靶心正下方,如图.只改变m、h、L、v0四个量中的一个,可能投中靶心的是( )
春节许多广场都有飞镖、空桶、套圈等项目.某同学在玩飞镖时,距地面高h、离靶面距离L处,将质量为m的飞镖以速度v0水平投出,落在靶心正下方,如图.只改变m、h、L、v0四个量中的一个,可能投中靶心的是( )
 春节许多广场都有飞镖、空桶、套圈等项目.某同学在玩飞镖时,距地面高h、离靶面距离L处,将质量为m的飞镖以速度v0水平投出,落在靶心正下方,如图.只改变m、h、L、v0四个量中的一个,可能投中靶心的是( )
春节许多广场都有飞镖、空桶、套圈等项目.某同学在玩飞镖时,距地面高h、离靶面距离L处,将质量为m的飞镖以速度v0水平投出,落在靶心正下方,如图.只改变m、h、L、v0四个量中的一个,可能投中靶心的是( )| A. | 适当增加v0 | B. | 适当增加m | C. | 适当提高h | D. | 适当增加L |
6. 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )| A. | 如果y表示加速度,则面积等于质点t0在时刻的速度 | |
| B. | 如果y表示流过用电器的电流,则面积等于在相应时间内该用电器消耗的电能 | |
| C. | 如果y表示力做功的功率,则面积等于该力在相应时间内所做的功 | |
| D. | 如果y表示变化磁场在金属线圈中产生的电动势,则面积等于该磁场在相应时间内磁感应强度的变化量 |
1.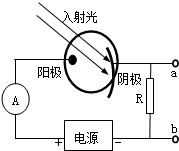 如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
 如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )
如图为光电管工作原理示意图,阴极材料的逸出功为W,入射光的光子能量为hv,能发生光电效应,则( )| A. | hv<W | |
| B. | 光电子在管内运动过程中电势能减小 | |
| C. | 减弱入射光强度,ab两端的电压减小 | |
| D. | 入射光的频率变高,所有出射光电子的动能都增大 |
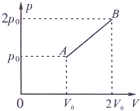 1mol理想气体的压强p与体积V关系如图所示.气体在状态A时的压强为p0、体积为V0,热力学温度为T0,在状态B时的压强为2p0,体积为2V0,AB为直线段.已知该气体内能与温度成正比U=CvT( Cv为比例系数).求:
1mol理想气体的压强p与体积V关系如图所示.气体在状态A时的压强为p0、体积为V0,热力学温度为T0,在状态B时的压强为2p0,体积为2V0,AB为直线段.已知该气体内能与温度成正比U=CvT( Cv为比例系数).求: