题目内容
电子所带电荷量的精确数值最早是由美国物理学家密立根于1917年通过油滴实验测得的.他测量了数千个带电油滴的电荷量,发现这些电荷量都是某个最小电荷量的整数倍.这个最小的电荷量就是电子所带的电荷量.
密立根实验的原理如图所示,A、B是两平行放置的水平金属板,A板带正电荷,B板带负电荷.从喷雾器嘴喷出的小油滴,从A板上的小孔落到A、B板之间的匀强电场中.如果小油滴带负电荷,它在电场中受竖直向下的重力和竖直向上的电场力作用,调节电场强度的大小(改变极板之间的电压),可以使油滴在A、B之间处于静止状态.
实验中用显微镜测得某油滴(可视为球体)的半径为R,当它处于静止状态时,电场强度为E.已知油的密度为ρ,重力加速度为g,球体的体积V=
πR3,求:
(1)该油滴重量的表达式.
(2)该油滴上所带电荷量的表达式.
(3)若该油滴的半径R=2.00×10-6m,当它处于静止状态时,电场强度E=2.00×105N/C.已知油的密度为ρ=0 80×103kg/m3,取重力加速度g=10m/s2,电子的电量e=1.60×10-19C,π=3,则该油滴上所带电荷量是电子电量的多少倍?
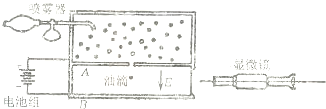
密立根实验的原理如图所示,A、B是两平行放置的水平金属板,A板带正电荷,B板带负电荷.从喷雾器嘴喷出的小油滴,从A板上的小孔落到A、B板之间的匀强电场中.如果小油滴带负电荷,它在电场中受竖直向下的重力和竖直向上的电场力作用,调节电场强度的大小(改变极板之间的电压),可以使油滴在A、B之间处于静止状态.
实验中用显微镜测得某油滴(可视为球体)的半径为R,当它处于静止状态时,电场强度为E.已知油的密度为ρ,重力加速度为g,球体的体积V=
| 4 | 3 |
(1)该油滴重量的表达式.
(2)该油滴上所带电荷量的表达式.
(3)若该油滴的半径R=2.00×10-6m,当它处于静止状态时,电场强度E=2.00×105N/C.已知油的密度为ρ=0 80×103kg/m3,取重力加速度g=10m/s2,电子的电量e=1.60×10-19C,π=3,则该油滴上所带电荷量是电子电量的多少倍?

分析:(1)根据密度定义公式、重量与质量的关系公式列式求解即可;
(2)油滴受重力和电场力平衡,根据平衡条件列式求解即可;
(3)用油滴的带电量除以元电荷即可.
(2)油滴受重力和电场力平衡,根据平衡条件列式求解即可;
(3)用油滴的带电量除以元电荷即可.
解答:解:(1)球形油滴的重量为:
G=mg=ρVg=ρ×
πR3×g=
πρR3g
(2)油滴静止时,根据平衡条件,有:
qE=mg
故:q=
=
(3)油滴的带电量是电子的n倍,有:
n=
=
=8
答:(1)该油滴重量的表达式为:G=
πρR3g.
(2)该油滴上所带电荷量的表达式为:q=
.
(3)该油滴上所带电荷量是电子电量的8倍.
G=mg=ρVg=ρ×
| 4 |
| 3 |
| 4 |
| 3 |
(2)油滴静止时,根据平衡条件,有:
qE=mg
故:q=
| G |
| E |
| 4πρR3g |
| 3E |
(3)油滴的带电量是电子的n倍,有:
n=
| q |
| e |
| 1.28×10-18C |
| 1.60×10-19C |
答:(1)该油滴重量的表达式为:G=
| 4 |
| 3 |
(2)该油滴上所带电荷量的表达式为:q=
| 4πρR3g |
| 3E |
(3)该油滴上所带电荷量是电子电量的8倍.
点评:本题关键是读懂题意,然后根据平衡条件列示求解;难点在于题目的信息量较大,要有耐心.

练习册系列答案
相关题目



