题目内容
(14分) 如图所示,固定在水平面上的斜面与水平面的连接处为一极小的光滑圆弧(物块经过Q点时不损失机械能),斜面与地面是用同种材料制成的。斜面的最高点为P,P距离水平面的高度为h=5m。在P点先后由静止释放两个可视为质点的小物块A和B,A、B的质量均为m=1kg,A与斜面及水平面的动摩擦因数为μ1=0.5,B与斜面及水平面的动摩擦因数为μ2=0.3。A物块从P点由静止释放后沿斜面滑下,停在了水平面上的某处。
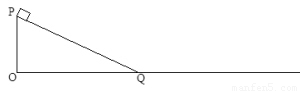
求:
(1)A物块停止运动的位置距离斜面的直角顶端O点的距离是多少?
(2)当A物块停止运动后准备再释放B物块时发现它们可能会发生碰撞,为了避免AB碰撞,此时对A另外施加了一个水平向右的外力F,把A物体推到了安全的位置,之后再释放B就避免了AB碰撞。求外力F至少要做多少功,可使AB不相撞?(g取10m/s2,此问结果保留三位有效数字)
【答案】
(1)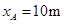 (2)
(2)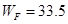 J
J
【解析】
试题分析:(1)设斜面倾角为θ,物块所停位置到Q点距离为S,A物块停止运动的位置距离斜面的直角顶端O点的距离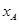 。
。
斜面长 ①
①
摩擦力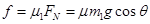 ②
②
由动能定理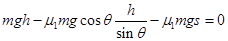 ③
③
停位置到O点距离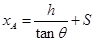 ④
④
由以上①②③④联立解得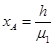 =10m ⑤
=10m ⑤
所以 A物块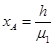 =10m ⑥
=10m ⑥
(2)若只释放B后,同理得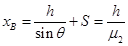 =16.7m ⑦
=16.7m ⑦
B比A多运动的距离为 =6.7m ⑧
=6.7m ⑧
若B与A不相碰应,将A至少向右推出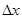 ,
,
由动能定理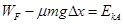 ⑨
⑨
当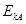 =0时WF最小
⑩
=0时WF最小
⑩
故至少做功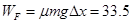 J ⑾
J ⑾
标准:③5分,⑤2分,⑥⑧⑩⑾各1分,⑨3分,共14分。
考点:动能定理

练习册系列答案
相关题目
 m/s2)求:
m/s2)求:

 =37°时立方体平衡且不动,作用在立方体上的水平推力F1应为多大?
=37°时立方体平衡且不动,作用在立方体上的水平推力F1应为多大?
 。一带正电
。一带正电 的小物块质量为m=0.5kg,它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,试求:(g=10m/s2)
的小物块质量为m=0.5kg,它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,试求:(g=10m/s2)