题目内容
在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α衰变,放出的α粒子的质量为m,电荷量为q,运动轨迹在与磁场垂直的平面内,且轨道半径为R.若原子核衰变时其能量都以α粒子和新核的动能形式释放,求它释放出的总能量(亏损的质量在与粒子质量相比时可忽略).
α粒子在洛伦兹力作用下做匀速圆周运动,由牛顿第二定律得
qvB=mv2/R,mv=qBR
设新核的速率为v′,忽略系统的质量亏损时的质量关系为M′=M-m
衰变过程中动量守恒,有
Mv=(M-m)v′
根据衰变时的能量转化和守恒,原子核释放的核能为:
ΔE=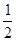
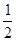mv2+(M-m)v′2
以上三式联立解得:ΔE=.
qvB=mv2/R,mv=qBR
设新核的速率为v′,忽略系统的质量亏损时的质量关系为M′=M-m
衰变过程中动量守恒,有
Mv=(M-m)v′
根据衰变时的能量转化和守恒,原子核释放的核能为:
ΔE=
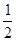mv2+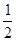(M-m)v′2以上三式联立解得:ΔE=
.
练习册系列答案
相关题目
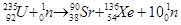
）发生核反应，生成氚核和α粒子，并释放出4.8Mev的能量（1u=931.5Mev）。
粒子和氚核的动能，且它们的动量等值反向，求
Th经过6次α衰变和4次β衰变后变成铅核，则（ ）
Pb，它比
Pb，它比
Pb，它比
发生
衰变时，设放出的能量都转变成了