题目内容
2.已知氢原子的基态能量为E1,量子数为n的激发态的能量为$\frac{{E}_{1}}{{n}^{2}}$.现有一群氢原子在向低能级跃迁过程中,其中从n=2能级向n=1能级跃迁辐射出的光子去轰击原来静止的电子,电子被射出后,光子反向运动,返回时光子的波长为λ1,普朗克常量为h,求跃迁辐射出的光子的波长λ0电子物质波的波长λ2.分析 (1)由氢原子的能级公式,结合波尔理论即可求出.
(2)根据动量守恒定律先求出电子的动量,然后代入物质波的波长公式即可;
解答 解:(1)n=2的能级的能量为:${E}_{2}=\frac{{E}_{1}}{{2}^{2}}=\frac{{E}_{1}}{4}$
从n=2能级向n=1能级跃迁辐射出的光子的能量为:E=E2-E1=$-\frac{3{E}_{1}}{4}$
根据光子的能量的公式:$E=\frac{hc}{λ}$
可得:${λ}_{0}=\frac{hc}{E}$=$-\frac{4hc}{3{E}_{1}}$
(2)光子与电子碰撞前的动量:${p}_{1}=\frac{E}{c}$=$\frac{h}{{λ}_{0}}$
碰撞后光子的能量:$E′=\frac{hc}{{λ}_{1}}$
则碰撞后的动量:${p}_{1}′=\frac{E′}{c}=\frac{h}{{λ}_{1}}$
光子与电子碰撞的前后动量守恒,以光子碰撞前的速度的方向为正方向,设碰撞后电子的动量是p2,则:
p1+0=-p1′+p2
根据物质波的波长的公式,可得电子的德布罗意波波长:${λ}_{2}=\frac{h}{{p}_{2}}$
联立以上各式,得:$\frac{h}{{λ}_{0}}+0=-\frac{h}{{λ}_{1}}+\frac{h}{{λ}_{2}}$
解得:λ2=$\frac{4hc{λ}_{1}}{4hc-3{E}_{1}{λ}_{1}}$
答:跃迁辐射出的光子的波长为$-\frac{4hc}{3{E}_{1}}$,电子物质波的波长为$\frac{4hc{λ}_{1}}{4hc-3{E}_{1}{λ}_{1}}$.
点评 该题以康普顿效应为基本情景,结合动量守恒定律比较全面第考查了光学与原子物理学的部分知识点的内容,虽然试题的难度不是特别大,但是也远超出了大纲对这一部分知识点的要求,在学习的过程中不需要对这一类的题目付出太多的时间.

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案 如图所示,MN是一半圆形绝缘线,等量异种电荷均匀分布在其上、下$\frac{1}{4}$圆弧上,O点为半圆的圆心,P为绝缘线所在圆上的一点,且OP垂直于MN,则下列说法正确的是( )
如图所示,MN是一半圆形绝缘线,等量异种电荷均匀分布在其上、下$\frac{1}{4}$圆弧上,O点为半圆的圆心,P为绝缘线所在圆上的一点,且OP垂直于MN,则下列说法正确的是( )| A. | 圆心O和圆上P点的电场强度大小相等,方向相同 | |
| B. | 圆心O和圆上P点的电场强度大小不相等,方向相同 | |
| C. | 将一负检验电荷沿直线从O运动到P,电场力先做正功后做负功 | |
| D. | 将一负检验电荷沿直线从O运动到P,电势能减小 |
| A. | 普朗克曾经大胆假设:振动着的带电微粒的能量只能是某一最小能量值ε的整数倍,这个不可再分的最小能量值ε叫做能量子 | |
| B. | 卢瑟福认为,原子是一个球体,正电荷弥漫性地均匀分布在整个球体内,电子镶嵌其中 | |
| C. | 按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hν,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek | |
| D. | 玻尔的原子理论第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了所有原子光谱的实验规律 | |
| E. | 德布罗意提出:实物粒子也具有波动性,而且粒子的能量ε和动量p跟它对所应的波的频率ν和波长λ之间,遵从关系v=$\frac{?}{h}$和λ=$\frac{h}{p}$ |
| 器材(代号) | 规格 |
| 电流表(A1) | 量程0~1mA,内阻约为50Ω |
| 电流表(A2) | 量程0~0.6A,内阻约为0.1Ω |
| 电压表(V1) | 量程0~3V,内阻约为10kΩ |
| 电压表(V2) | 量程0~15V,内阻约为50kΩ |
| 滑动变阻器(R) | 阻值范围0~50Ω, 允许最大电流0.5A |
| 直流电源(E) | 输出电压15V,内阻不计 |
| 开关(S)、导线若干 | |
| 毫米刻度尺、游标卡尺 | |
| 多用电表 | |
| 一节两端可封 住的绝缘PVC水管 |

(1)用毫米刻度尺测量如图1所示的一段自来水管上两接线柱间距离为L; 用游标卡尺测量水管内径为d;
(2)用多用电表测量两接线柱间装满自来水电阻约20kΩ;为提高实验结果的准确程度,电流表应选用A1,电压表应选用V2(以上均填器材代号);
(3)为了达到上述目的,某同学设计出正确的电路原理图,并按电路图连接好实物图,如图2所示.接通电路后,当调节滑动变阻器的滑片时,发现电压表、电流表有示数但几乎不变,请指出哪一根导线发生了断路?c(只填写图中导线字母代号);
(4)若实验电路中电流表示数为I,电压表示数为U,可求得自来水的电阻率ρ=$\frac{{πd}_{\;}^{2}U}{4IL}$.(用以上测得的物理量符号表示)
| A. | 一般抛体运动均可分解为两个直线运动 | |
| B. | 平抛运动在某个时刻的加速度可能与速度方向相同 | |
| C. | 做直线运动的物体受到的合外力不一定是恒力 | |
| D. | 做平抛运动的物体在不同时间内速度变化的方向是相同的 |
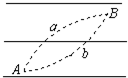 如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )
如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1J,若A点电势为-10V,则( )| A. | B点电势为零 | B. | 电场线方向向左 | ||
| C. | 电荷运动的轨迹可能是图中曲线a | D. | 电荷运动的轨迹可能是图中曲线b |
 用油膜法估测分子的大小,方法及步骤如下:
用油膜法估测分子的大小,方法及步骤如下: