题目内容
【题目】如图所示，有一电子（电量为e、质量为m）经电压U加速后，沿平行金属板A、B中心线进入两板，A、B板间距为d、长度为L，A、B板间电压也为U，屏CD足够大，距离A、B板右边缘3L，AB板的中心线过屏CD的中心且与屏CD垂直．试求电子束打在屏上的位置到屏中心间的距离．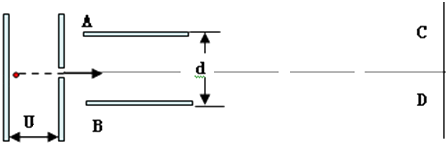
【答案】解：设电子经加速电场加速后获得速度v0 ， 经过偏转电场偏转后发生偏移量y，速度偏转角为θ，电子打在屏上的位置到屏中心间的距离为y1 ， 则：
加速电场中有动能定理得： 
，解得： 
…①，
粒子在AB板间运动过程：水平方向由：L=v0t解得： 
…②，
竖直方向： 
…③，
= 
= 
…④，
vy=at= 
…⑤，
= 
= 
…⑥，
离开偏转场后电子匀速飞向屏的过程： 
…⑦，
由①～⑦解得： 
．
【解析】粒子在加速电场中做匀加速运动在偏转电场中做类平抛运动，出电场后做匀速直线运动，利用偏转知识求解偏转位移，借助偏转夹角求解无电场区域的位移，两者之和即为结果；
【考点精析】解答此题的关键在于理解带电微粒（计重力）在电场中的运动的相关知识，掌握带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法．
练习册系列答案
备战中考寒假系列答案
相关题目
