题目内容
18. 如图所示,一小球以初速度v0沿水平方向射出,恰好垂直地射到一倾角为30°的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的$\frac{3}{4}$,则下列说法正确的是( )
如图所示,一小球以初速度v0沿水平方向射出,恰好垂直地射到一倾角为30°的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的$\frac{3}{4}$,则下列说法正确的是( )| A. | 小球在竖直方向下落的距离与在水平方向通过的距离的比为$\sqrt{3}$ | |
| B. | 水平射出后经$\frac{{2v}_{0}}{g}$秒垂直撞到斜面 | |
| C. | 在碰撞中小球的速度变化大小为$\frac{1}{2}$v0 | |
| D. | 在碰撞中小球的速度变化大小为$\frac{7}{2}$v0 |
分析 根据平行四边形定则求出小球与斜面碰撞前的竖直分速度大小以及速度大小,从而求出碰撞过程中速度的变化量大小.根据运动的时间,求出小球竖直位移和水平位移,从而求出竖直方向上下落的距离和水平方向上通过的距离比.
解答 解:A、小球垂直撞在斜面上,速度与竖直方向的夹角为30°,根据平行四边形定则知:tan30°=$\frac{{v}_{0}}{{v}_{y}}$,得:vy=$\sqrt{3}{v}_{0}$
小球在竖直方向下落的距离 y=$\frac{{v}_{y}}{2}t$=$\frac{\sqrt{3}}{2}{v}_{0}t$,在水平方向通过的距离 x=v0t,则 y:x=$\sqrt{3}$:2,故A错误.
B、由vy=gt得 t=$\frac{\sqrt{3}{v}_{0}}{g}$,即水平射出后经$\frac{\sqrt{3}{v}_{0}}{g}$秒垂直撞到斜面,故B错误.
CD、由sin30°=$\frac{{v}_{0}}{{v}_{1}}$,解得小球与斜面碰撞前的速度大小 v1=2v0,取撞击斜面前速度方向为正,则碰撞过程中的速度变化量△v=-$\frac{3}{4}{v}_{1}$-v1=-$\frac{7}{4}×2{v}_{0}$=-$\frac{7}{2}$v0,大小为$\frac{7}{2}$v0,故C错误,D正确.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道分速度与合速度之间遵守平行四边形定则.

练习册系列答案
相关题目
8. 如图所示,直流电动机线圈的电阻为R,电源内阻为r,当该电动机正常工作时,电源路端电压为U,通过电动机的电流为I,则( )
如图所示,直流电动机线圈的电阻为R,电源内阻为r,当该电动机正常工作时,电源路端电压为U,通过电动机的电流为I,则( )
 如图所示,直流电动机线圈的电阻为R,电源内阻为r,当该电动机正常工作时,电源路端电压为U,通过电动机的电流为I,则( )
如图所示,直流电动机线圈的电阻为R,电源内阻为r,当该电动机正常工作时,电源路端电压为U,通过电动机的电流为I,则( )| A. | 电源的输出功率为IU+I2R | B. | 电动机的机械功率为IU | ||
| C. | 电源电动势为I(R+r) | D. | 电动机内部发热功率为I2R |
9.人类正在有计划地探索地球外其他星球,若宇宙空间某处有质量均匀分布的实心球形天体,宇航员在星球上可完成以下工作;1、测得A物体质量.2、测出离球面已知高度h平抛物体落地时间t.3、观测其卫星匀速圆周运动的周期T.4、测出此卫星离球面高度H.5、用弹簧测力计测得A物体在该天体的极地比赤道上重P,已知引力常量G.则下列有关推断正确的是( )
| A. | 由3、4可推知星球质量 | |
| B. | 由1、5可推知星球同步卫星周期 | |
| C. | 由2、3、4可推知星球的第一宇宙速度 | |
| D. | 由1、2、5可推知该天体的密度 |
3. 如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
 如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
如图质量为m的小球用水平弹簧系住,并用倾角为37°的光滑木板AB托住,小球恰好处于静止状态.已知sin37°=0.6,cos37°=0.8,重力加速度为g.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )| A. | 大小为0 | B. | 大小为0.75g | C. | 大小为g | D. | 大小为1.25g |
10.一石块从楼顶自由落下.不计空气阻力,取 g=10m/s2.在石块下落的过程中( )
| A. | 第 1 s 内下落的高度为 1 m | B. | 第 1 s 内下落的高度为 5 m | ||
| C. | 第 1 s 内下落的高度为 10 m | D. | 第 1 s 内下落的高度为 15 m |
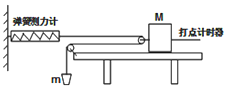 为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置,其中M为带滑轮的小车的质量,m为砂和砂桶的质量,(滑轮质量不计)
为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置,其中M为带滑轮的小车的质量,m为砂和砂桶的质量,(滑轮质量不计) 现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流表、开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现他将滑动变阻器的滑动端P向左加速滑动时,电流表指针向右偏转,由此可以判断:线圈A向上移动都能引起电流表指针右偏转.线圈A中铁芯向上拔出或断开开关,都能引起电流表指针右偏转(填向右或左)
现将电池组、滑动变阻器、带铁芯的线圈A、线圈B、电流表、开关如图连接.在开关闭合、线圈A放在线圈B中的情况下,某同学发现他将滑动变阻器的滑动端P向左加速滑动时,电流表指针向右偏转,由此可以判断:线圈A向上移动都能引起电流表指针右偏转.线圈A中铁芯向上拔出或断开开关,都能引起电流表指针右偏转(填向右或左)