题目内容
8.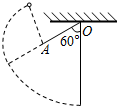 如图所示,摆球质量为m,摆长为L,悬挂在O点,在摆球运动的竖直平面内A点处固定一个钉子,OA=$\frac{L}{2}$,OA与竖直方向成60°角,求摆球在最低点至少具有多大速度才能使摆球上摆时绕A点在竖直平面内作圆周运动.
如图所示,摆球质量为m,摆长为L,悬挂在O点,在摆球运动的竖直平面内A点处固定一个钉子,OA=$\frac{L}{2}$,OA与竖直方向成60°角,求摆球在最低点至少具有多大速度才能使摆球上摆时绕A点在竖直平面内作圆周运动.
分析 小球做圆周运动,运动到A处与钉子相碰,碰后做半径为L的圆周运动,要使它能够做完整的圆周运动,则当小球正好通过最高点时,由重力提供向心力时,速度最小,根据牛顿第二定律结合动能定理即可求解.
解答 解:绳子碰到A点后以A点为圆心,$\frac{L}{2}$为半径,在竖直平面内做圆周运动,要使摆球上摆时绕A点在竖直平面内作完整的圆周运动,则在最高点,当重力提供向心力时,速度最小,则有:
mg=m$\frac{{v}^{2}}{\frac{L}{2}}$
解得:v=$\sqrt{\frac{gL}{2}}$
从最低点到最高点的过程中,根据动能定理得:
$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}=-mg(2L-Lsin30°+L)$
解得:${v}_{0}=\sqrt{\frac{11gL}{2}}$
答:摆球在最低点至少具有$\sqrt{\frac{11gL}{2}}$的速度才能使摆球上摆时绕A点在竖直平面内作圆周运动.
点评 本题主要考查了向心力公式以及动能定理的直接应用,知道要小球能够绕A点做完整的圆周运动,当正好通过最高点时,由重力提供向心力,速度最小,难度适中.

练习册系列答案
相关题目
18.实践证明,开普勒定律不仅适用于太阳系中的天体运动,而且对一切天体(包括卫星绕行星的运动)都适用.下面对于开普勒第三定律的公式$\frac{{R}^{3}}{{T}^{2}}$=T,说法正确的是( )
| A. | 式中的k值,中与中心天体有关,与绕中心天体旋转的行星(或卫星)无关 | |
| B. | 公式只适用于轨道是椭圆的运动 | |
| C. | 式中的k值,对于所有行星(或卫星)都相等 | |
| D. | 若已知月球与地球之间的距离,根据公式可求出地球与太阳之间的距离 |
16.关于功率,下列说法正确的是( )
| A. | 由P=$\frac{W}{t}$可知,只要知道W和t就可以求出任意时刻的功率 | |
| B. | 由P=Fv可知,汽车的功率是与它的速度成正比的 | |
| C. | 由P=Fv可知,当发动机功率一定时,牵引力与速度成反比 | |
| D. | 由P=Fv可知,通过减小牵引力,可使汽车的速度一直增大 |
13. 如图所示,在固定斜面上的物块受到一平行于斜面向上的外力F的作用,物块能够在斜面上保持静止的力的范围为3N≤F≤5N,取g=10m/s2,由此可知( )
如图所示,在固定斜面上的物块受到一平行于斜面向上的外力F的作用,物块能够在斜面上保持静止的力的范围为3N≤F≤5N,取g=10m/s2,由此可知( )
 如图所示,在固定斜面上的物块受到一平行于斜面向上的外力F的作用,物块能够在斜面上保持静止的力的范围为3N≤F≤5N,取g=10m/s2,由此可知( )
如图所示,在固定斜面上的物块受到一平行于斜面向上的外力F的作用,物块能够在斜面上保持静止的力的范围为3N≤F≤5N,取g=10m/s2,由此可知( )| A. | 物块的质量m=0.8kg | B. | 物块的质量m=0.4kg | ||
| C. | 物块与斜面间的最大静摩擦力为1N | D. | 物块与斜面间的最大静摩擦力为4N |
20.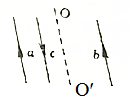 如图所示,a、b为两条固定的平行直导线,导线通以方向相同、大小相等的电流,导线c与a,b平行,且可在a、b所决定的平面内移动,OO′是在a、b平面内.与a、b平行且等距的中心线,当c中通以与a、b反向的电流之后,下列判断正确的是( )
如图所示,a、b为两条固定的平行直导线,导线通以方向相同、大小相等的电流,导线c与a,b平行,且可在a、b所决定的平面内移动,OO′是在a、b平面内.与a、b平行且等距的中心线,当c中通以与a、b反向的电流之后,下列判断正确的是( )
 如图所示,a、b为两条固定的平行直导线,导线通以方向相同、大小相等的电流,导线c与a,b平行,且可在a、b所决定的平面内移动,OO′是在a、b平面内.与a、b平行且等距的中心线,当c中通以与a、b反向的电流之后,下列判断正确的是( )
如图所示,a、b为两条固定的平行直导线,导线通以方向相同、大小相等的电流,导线c与a,b平行,且可在a、b所决定的平面内移动,OO′是在a、b平面内.与a、b平行且等距的中心线,当c中通以与a、b反向的电流之后,下列判断正确的是( )| A. | b所受磁场力一定为零 | B. | c将一直受到磁场力作用 | ||
| C. | c将向右运动,停在OO′的位置 | D. | c将在OO′左右来回振动 |
17.下列说法符合历史事实的是( )
| A. | 爱因斯坦发现了“万有引力定律” | |
| B. | 亚里士多德提出了“日心说” | |
| C. | 第谷通过长期的天文观测发现了行星运动的三大定律 | |
| D. | 卡文迪许精确的测出引力常量G,因此被称为“能称出地球质量的人” |

