题目内容
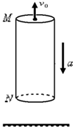如图，离地面足够高处有一竖直的空管，质量为m=2kg，管长为L=24m，M、N为空管的上、下两端，空管受到F=16N竖直向上的拉力作用，由静止开始竖直向下做加速运动，空管下落的同时，在M处将一个大小不计的小球，沿管的轴线以大小为v0=10m/s初速度竖直上抛，不计空气阻力．取g=10m/s2．求小球经过多长时间从管的N端穿出？分析：管匀加速下降，球先减速下降后加上升，整个过程为匀变速运动，根据位移时间公式结合几何关系列式求解即可
解答：解：对管，根据牛顿第二定律，有
mg-F=ma
根据运动学公式，有
h=
at2
对小球，以向上为正，根据位移时间公式，有
-（h+L）=v0t-
gt2
解得：t=4s
答：经过4s时间小球从管的N端穿出．
mg-F=ma
根据运动学公式，有
h=
| 1 |
| 2 |
对小球，以向上为正，根据位移时间公式，有
-（h+L）=v0t-
| 1 |
| 2 |
解得：t=4s
答：经过4s时间小球从管的N端穿出．
点评：本题关键要将小球运动的整个过程看成匀变速直线运动，如果分段考虑，将使问题变得复杂化．
练习册系列答案
计算高手系列答案
相关题目
（2011?天门二模）如图所示，离地面足够高处有一竖直的空管，质量为2kg，管长为24m，M、N为空管的上、下两端，空管受到F=16N竖直向上的拉力作用，由静止开始竖直向下做加速运动，同时在M处一个大小不计的小球沿管的轴线以初速度v0竖直上抛，不计一切阻力，取g=10m/s2．求：
如图所示，离地面足够高处有一用绳连接的竖直空管，管长为24m，M、N为空管的上、下两端，空管以a=2m/s2的加速度由静止开始竖直向下做加速运动，同时在M处一个大小不计的小球沿管的轴线以初速度v0竖直上抛，不计一切阻力，取g=10m/s2．求：
（2009?上海模拟）如图所示，离地面足够高处有一竖直的空心管，质量为2kg，管长为24m，M、N为空心管的上、下两端，空心管受到大小为16N的竖直向上的拉力作用，由静止开始竖直向下做匀加速运动，同时在M处有一个大小不计的小球沿管的轴线做竖直上抛运动，取g=10m/s2．若小球上抛的初速度为10m/s，经过
如图，离地面足够高处有一竖直的空管，质量为m=2kg，管长为L=24m，M、N为空管的上、下两端，空管受到F=16N竖直向上的拉力作用，由静止开始竖直向下做加速运动，空管下落的同时，在M处将一个大小不计的小球，沿管的轴线以大小为v0=10m/s初速度竖直上抛，不计空气阻力．取g=10m/s2．求小球经过多长时间从管的N端穿出？