题目内容
一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示。试问:在这段时间内电梯上升的高度是多少?取重力加速度g=10m/s2。
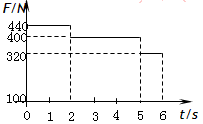
解:由图可知,在t=0到t1=2s的时间内,体重计的示数大于mg,故电梯应做向上的加速运动。
设在这段时间内体重计作用于小孩的力为f1,电梯及小孩的加速度为a1,
根据牛顿第二定律,得:f1-mg=ma1 ①
在这段时间内电梯上升的高度h1=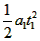 ②
②
在t1到t=t2=5s的时间内,体重计的示数等于mg,
故电梯应做匀速上升运动,速度为t1时刻的电梯的速度,即v1=a1t1 ③
在这段时间内电梯上升的高度h1=v1t2 ④
在t2到t=t3=6s的时间内,体重计的示数小于mg,故电梯应做减速上升运动。
设这段时间内体重计作用于小孩的力为f2,电梯及小孩的加速度为a2,
由牛顿第二定律,得:mg-f2=ma2⑤
在这段时间内电梯上升的高度h3=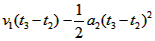 ⑥
⑥
电梯上升的总高度h=h1+h2+h3 ⑦
由以上各式,利用牛顿第三定律和题文及题图中的数据,解得h=9m。
设在这段时间内体重计作用于小孩的力为f1,电梯及小孩的加速度为a1,
根据牛顿第二定律,得:f1-mg=ma1 ①
在这段时间内电梯上升的高度h1=
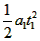 ②
② 在t1到t=t2=5s的时间内,体重计的示数等于mg,
故电梯应做匀速上升运动,速度为t1时刻的电梯的速度,即v1=a1t1 ③
在这段时间内电梯上升的高度h1=v1t2 ④
在t2到t=t3=6s的时间内,体重计的示数小于mg,故电梯应做减速上升运动。
设这段时间内体重计作用于小孩的力为f2,电梯及小孩的加速度为a2,
由牛顿第二定律,得:mg-f2=ma2⑤
在这段时间内电梯上升的高度h3=
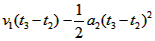 ⑥
⑥ 电梯上升的总高度h=h1+h2+h3 ⑦
由以上各式,利用牛顿第三定律和题文及题图中的数据,解得h=9m。

练习册系列答案
相关题目
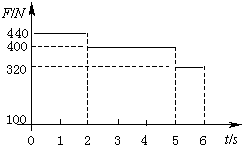 (2006?甘肃)一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.
(2006?甘肃)一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.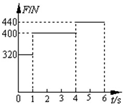 一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始下降,在0到6s内体重计示数F的变化如图所示.
一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始下降,在0到6s内体重计示数F的变化如图所示. 一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0s到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?(取重力加速度g=10m/s2.)
一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0s到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?(取重力加速度g=10m/s2.)