题目内容
【题目】如图所示,在光滑的水平地面上,相距L=10 m的A、B两个小球均以v0=10 m/s向右运动,随后两球相继滑上倾角为30°的足够长的光滑斜坡,地面与斜坡平滑连接,取g=10 m/s2。求:
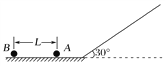
(1)B球刚要滑上斜坡时A、B两球的距离;
(2)A球滑上斜坡后经过多长时间两球相遇。
【答案】(1)7.5 m (2)2.5 s
【解析】试题分析:根据位移公式求出B球刚滑上斜坡时A球滑上斜坡的时间,根据牛顿第二定律和运动学公式求出A上滑的位移,从而得出A、B两球的距离;根据速度时间公式求出B球滑上斜坡时A球的速度,得出B相对A的速度,结合位移公式求出相遇的时间。
(1)设A球滑上斜坡后经过t1时间B球滑上斜坡,则有:![]()
解得:![]()
A球滑上斜坡后加速度:a=gsin 30°=5m/s2
设这段时间内A球向上运动的位移为x,则![]()
代入数据解得:![]()
(2)B球刚要滑上斜坡时A球速度v1=v0-at1=5m/s
B球滑上斜坡时,加速度与A相同,以A为参考系,
B相对于A以v=v0-v1=5 m/s做匀速运动,
设再经过时间t2它们相遇,有:![]()
则相遇时已经过的时间t=t1+t2=2.5 s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目