Question

【题目】如图所示，在光滑的水平地面上有一个表面光滑的立方体M，一轻杆L与水平地面成角，轻杆的下端用光滑铰链连接于O点，O固定于地面上，轻杆的上端连接质量为m的小球，小球靠在立方体左侧，立方体右侧受到水平向左推力F的作用。整个装置处于静止状态。若现在撤去水平推力F，则下列说法中正确的是（ ）

A.在小球和立方体分离前，小球速率等于立方体速率

B.小球和立方体分离时小球加速度为零

C.小球在落地的瞬间和立方体分离

D.小球和立方体分离时小球只受重力

Answer 1

【答案】D

【解析】

小球一方面随着立方体向右运动，一方面竖直向下运动，将小球的速度沿着水平方向和竖直方向正交分解，可以得到小球在水平方向的分速度；再对整体在水平方向上应用牛顿第二定律分析。

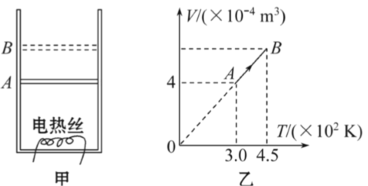
A．将小球的运动分解为水平方向和竖直方向，小球水平方向的速度与立方体的速度相等：

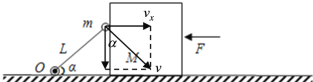
根据图中分解速度可知：

小球的速率大于立方体的速率，故A错误；

B．二者分离时，小球做圆周运动，加速度不为零，故B错误；

C．分离瞬间小球速度水平分量等于立方体的速度，所以立方体会在小球落在水平地面之前离开小球，故C错误；

D．分离瞬间，小球与物块在弹力方向上的速度和加速度相同，也就是水平方向上小球和物块的加速度相同，物块的加速度为0，小球在水平方向上的加速度也为0，那么杆对小球的作用力为0，所以小球只受重力，故D正确。