题目内容
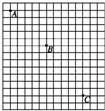 如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:两次闪光的时间间隔为
如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:两次闪光的时间间隔为分析:小球做平抛运动,运用运动的分解方法研究:竖直的分运动是自由落体运动,根据匀加速运动的推论△y=aT2求出两次闪光的时间间隔,再由两点水平方向的位移大小求初速度.由匀速直线运动的推论求出B点竖直方向的分速度,从而求出从抛出到A点的时间,即可得到水平距离.
解答:解:设两次闪光的时间间隔为T,每个方格的边长为L.竖直方向上小球做自由落体运动,则得:
yBC-yAB=gT2
由图看出:yBC-yAB=7L-5L=2L=10cm=0.1m
联立以上两式得:T=0.1s
水平方向上小球做匀速直线运动,则得:xAB=5L=v0T,则得:v0=
=
m/s=2.5m/s
B点的竖直分速度为:vB=
=
=
m/s=3m/s
所以从抛出到B的时间为:tB=
=
s=0.3s
从抛出到A点的时间为:tA=tB-T=0.3-0.1=0.2s,
故小球做平抛运动的初始点O离A点的水平距离为:x=v0tA=2.5×0.2m=0.5m
故答案为:0.1,2.5,0.5.
yBC-yAB=gT2
由图看出:yBC-yAB=7L-5L=2L=10cm=0.1m
联立以上两式得:T=0.1s
水平方向上小球做匀速直线运动,则得:xAB=5L=v0T,则得:v0=
| 5L |
| T |
| 5×0.05 |
| 0.1 |
B点的竖直分速度为:vB=
| hAB+hBC |
| 2T |
| 5L+7L |
| 2T |
| 6×0.05 |
| 0.1 |
所以从抛出到B的时间为:tB=
| vB |
| g |
| 3 |
| 10 |
从抛出到A点的时间为:tA=tB-T=0.3-0.1=0.2s,
故小球做平抛运动的初始点O离A点的水平距离为:x=v0tA=2.5×0.2m=0.5m
故答案为:0.1,2.5,0.5.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
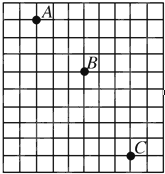 如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:闪光频率为
如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:闪光频率为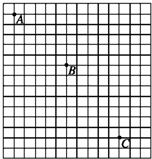 如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:闪光频率为
如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:闪光频率为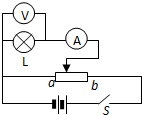 用如图所示的电路图研究小灯泡L(2.4V,1.0W)的伏安特性曲线,并测出该灯泡在额定电压下正常工作时的电阻值,检验其标称的准确性.
用如图所示的电路图研究小灯泡L(2.4V,1.0W)的伏安特性曲线,并测出该灯泡在额定电压下正常工作时的电阻值,检验其标称的准确性.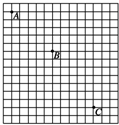 如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:小球抛出时的初速度大小为
如图所示的是“研究小球的平抛运动”时拍摄的闪光照片的一部分,其背景是边长为5cm的小方格,取g=10m/s2.由此可知:小球抛出时的初速度大小为