题目内容
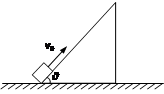
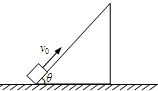 足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,取g=10m/s2)求:
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,取g=10m/s2)求:(1)物体上滑过程中的加速度.
(2)物体上滑过程的最大位移.
(3)物体从开始到再次返回斜面底端所需的时间.
分析:(1)根据牛顿第二定律列式,求解加速度.
(2)当物体的速度减为零时位移达到最大,由匀变速运动的位移速度关系公式求解最大位移.
(3)根据牛顿第二定律求出物体下滑过程的加速度,抓住下滑与上滑位移大小相等,由位移公式求出下滑时间,再由速度公式求上滑时间,即可求得总时间.
(2)当物体的速度减为零时位移达到最大,由匀变速运动的位移速度关系公式求解最大位移.
(3)根据牛顿第二定律求出物体下滑过程的加速度,抓住下滑与上滑位移大小相等,由位移公式求出下滑时间,再由速度公式求上滑时间,即可求得总时间.
解答:解:(1)由牛顿第二定律 上滑过程中:mgsinθ+μmgcosθ=ma
得a=gsinθ+μgcosθ=(10×0.8+0.8×10×0.6)m/s2=12.8m/s2
(2)上滑最大距离:x=
=
m=1.6m
(3)上滑时间:t1=
=
s=0.5s
下滑过程中:mgsinθ-μmgcosθ=ma′
得 a′=gsinθ-μgcosθ=(8-4.8)m/s2=3.2m/s2
又根据x=
a′t22下滑时间t2=
=
=1s
总时间为:t=t1+t2=1.5s
答:
(1)物体上滑过程中的加速度是12.8m/s2.
(2)物体上滑过程的最大位移是1.6m.
(3)物体从开始到再次返回斜面底端所需的时间是1.5s.
得a=gsinθ+μgcosθ=(10×0.8+0.8×10×0.6)m/s2=12.8m/s2
(2)上滑最大距离:x=
| v02 |
| 2a |
| 6.42 |
| 2×12.8 |
(3)上滑时间:t1=
| v0 |
| a |
| 6.4 |
| 12.8 |
下滑过程中:mgsinθ-μmgcosθ=ma′
得 a′=gsinθ-μgcosθ=(8-4.8)m/s2=3.2m/s2
又根据x=
| 1 |
| 2 |
|
|
总时间为:t=t1+t2=1.5s
答:
(1)物体上滑过程中的加速度是12.8m/s2.
(2)物体上滑过程的最大位移是1.6m.
(3)物体从开始到再次返回斜面底端所需的时间是1.5s.
点评:本题是两个过程的问题,运用牛顿第二定律和运动学规律结合进行处理,还要抓住两个过程的位移大小相等.

练习册系列答案
相关题目
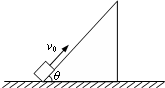 足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2) (2008?淮安模拟)足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)
(2008?淮安模拟)足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)