题目内容
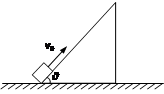
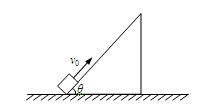
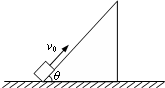 足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)(1)求上滑与下滑过程中的加速度a1,a2
(2)求物体从开始到再次返回斜面底端所需的时间;
(3)求返回斜面底端时的速度;
(4)若仅将斜面倾角θ变为37°,其他条件不变,试求物体在开始第1s内的位移大小.(结果保留2位有效数字)
分析:(1)根据动能定理求解物体上滑的最大距离,再根据牛顿第二定律求出物体下滑过程的加速度大小,由位移公式x=
at2求出物体返回斜面底端的时间.
(2)根据动能定理求解物体下滑到底端时的速度
(3)先计算上滑时间与1s比较得出物体处于什么运动状态,另外比较重力沿斜面向下的分力与最大静摩擦力比较,看滑到最高点后能否下滑,然后利用匀变速直线运动规律即可求解.
| 1 |
| 2 |
(2)根据动能定理求解物体下滑到底端时的速度
(3)先计算上滑时间与1s比较得出物体处于什么运动状态,另外比较重力沿斜面向下的分力与最大静摩擦力比较,看滑到最高点后能否下滑,然后利用匀变速直线运动规律即可求解.
解答:解:(1)物体上滑过程,根据动能定理得
-(mgxsinθ+μmgcosθ)x=0-
mv02 ①
根据牛顿第二定律得,
物体上滑过程的加速度大小为a1=
=g(sinθ+μcosθ)=10×(0.8+0.8×0.6)m/s2=12.8m/s2 ②
物体下滑过程的加速度大小为a2=
=g(sinθ-μcosθ)=10×(0.8-0.8×0.6)m/s2=3.2m/s2 ③
由公式x=
at2得:
物体上滑所用时间为 t1=
④
物体下滑时间为t2=
⑤
物体从开始到再次返回斜面底端所需的时间 t=t1+t2 ⑥
①→⑥联立得:t=1.5s
(2)物体下滑过程,根据动能定理得
(mgxsinθ-μmgcosθ)x=
mv2 ⑦
①⑦联立得:v=3.2m/s
(3)当θ=37°时由牛顿第二定律得:
物体上滑过程的加速度大小为a1′=
=g(sinθ+μcosθ)=10×(0.6+0.8×0.8)m/s2=12.4m/s2
上滑时间:t1′=
=
s=
s<1s
又因为tanθ=0.75<0.8 所以物体滑到最顶端后不再下滑,保持静止.
得物体在开始第1s内的位移大小:x′=
=
m=1.7m
答:(1)求物体从开始到再次返回斜面底端所需的时间为1.5s;
(2)求返回斜面底端时的速度3.2m/s;
(3)物体在开始第1s内的位移大小为1.7m.
-(mgxsinθ+μmgcosθ)x=0-
| 1 |
| 2 |
根据牛顿第二定律得,
物体上滑过程的加速度大小为a1=
| mgsinθ+μmgcosθ |
| m |
物体下滑过程的加速度大小为a2=
| mgsinθ-μmgcosθ |
| m |
由公式x=
| 1 |
| 2 |
物体上滑所用时间为 t1=
|
物体下滑时间为t2=
|
物体从开始到再次返回斜面底端所需的时间 t=t1+t2 ⑥
①→⑥联立得:t=1.5s
(2)物体下滑过程,根据动能定理得
(mgxsinθ-μmgcosθ)x=
| 1 |
| 2 |
①⑦联立得:v=3.2m/s
(3)当θ=37°时由牛顿第二定律得:
物体上滑过程的加速度大小为a1′=
| mgsinθ+μmgcosθ |
| m |
上滑时间:t1′=
| v0 |
| a′1 |
| 6.4 |
| 12.1 |
| 16 |
| 31 |
又因为tanθ=0.75<0.8 所以物体滑到最顶端后不再下滑,保持静止.
得物体在开始第1s内的位移大小:x′=
| v′02 |
| 2a′1 |
| 6.42 |
| 2×12.4 |
答:(1)求物体从开始到再次返回斜面底端所需的时间为1.5s;
(2)求返回斜面底端时的速度3.2m/s;
(3)物体在开始第1s内的位移大小为1.7m.
点评:本题是两个过程的问题,运用动能定理、牛顿第二定律和运动学规律结合进行处理,还要抓住两个过程的位移大小相等.

练习册系列答案
相关题目
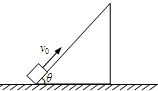 足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,取g=10m/s2)求:
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,取g=10m/s2)求: (2008?淮安模拟)足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)
(2008?淮安模拟)足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4m/s的初速度,从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10m/s2)