题目内容
【题目】现有一根长度为L=15m、质量分布均匀的长方体木板，已知重力加速度为g=10m/s2，完成下列问题：
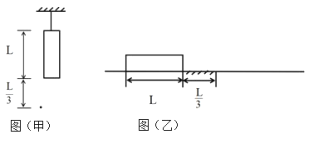
（1）若将该木板竖直悬挂，如图（甲）所示，由静止释放后，不考虑空气阻力，求木板通过其正下方
处一标记点的时间；
（2）若将该木板置于水平面上，如图（乙）所示，水平面上有长为的一段粗糙区域，其它区域光滑，已知木板与粗糙区域间的动摩擦因数为μ=0.25，木板与粗糙区域间正压力与木板在该区域的长度成正比，现给木板一初速度，求使木板能通过该粗糙区域的最小初速度。
【答案】（1）1s；（2）5m/s
【解析】
（1）木板下端从释放到标记点
木板上端从释放到标记点
木板通过标记点的时间
（2）以木板从刚开始进入粗糙区域为起点，木板的位移为x，质量为m
①当
时，木板与粗糙区域摩擦力
克服摩擦力做功
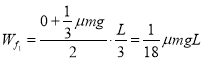
②当
时，木板与粗糙区域摩擦力
克服摩擦力做功
③当
时，木板与粗糙区域摩擦力与过程①类似
克服摩擦力做功
全过程由动能定理
解得
=5m/s
练习册系列答案
相关题目
