题目内容
 如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上从静止开始向右运动,运动5.2m后撤去外力F.已知力F与水平方向的夹角θ=37°,sin 37°=0.6,cos 37°=0.8,g 取 10m/s2.求:
如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上从静止开始向右运动,运动5.2m后撤去外力F.已知力F与水平方向的夹角θ=37°,sin 37°=0.6,cos 37°=0.8,g 取 10m/s2.求:(1)撤去外力前,木块受到的摩擦力大小;
(2)刚撤去外力时,木块运动的速度;
(3)撤去外力后,木块还能滑行的距离为多少?
分析:(1)对球受力分析知,其受重力,拉力,支持力,摩擦力,由竖直的平衡和摩擦力表达式可得摩擦力
(2)由动能定理可得撤去外力时的速度
(3)由动能定理可得撤去后的位移
(2)由动能定理可得撤去外力时的速度
(3)由动能定理可得撤去后的位移
解答:解:
(1)对小球:N+Fsin37°=mg
f=μN
由以上方程解得:f=μ(mg-Fsin37°)=0.2×(2×10-10×0.6)=2.8N
(2)对木块,根据动能定理:(Fcos37°-f)S1=
mv2
(10×0.8-2.8)×5.2=
×2×v2
解得:v═5.2m/s
(3)对木块撤去外力后,根据动能定理:-μmgS2=0-
mv2
0.2×2×10×s2=
×2×5.22
解得:S2=6.76m
答:
(1)撤去外力前,木块受到的摩擦力大小2.8N
(2)刚撤去外力时,木块运动的速度5.2m/s
(3)撤去外力后,木块还能滑行的距离为6.76m
(1)对小球:N+Fsin37°=mg
f=μN
由以上方程解得:f=μ(mg-Fsin37°)=0.2×(2×10-10×0.6)=2.8N
(2)对木块,根据动能定理:(Fcos37°-f)S1=
| 1 |
| 2 |
(10×0.8-2.8)×5.2=
| 1 |
| 2 |
解得:v═5.2m/s
(3)对木块撤去外力后,根据动能定理:-μmgS2=0-
| 1 |
| 2 |
0.2×2×10×s2=
| 1 |
| 2 |
解得:S2=6.76m
答:
(1)撤去外力前,木块受到的摩擦力大小2.8N
(2)刚撤去外力时,木块运动的速度5.2m/s
(3)撤去外力后,木块还能滑行的距离为6.76m
点评:本题是简单的动能定理的应用,属于非常基础的题目.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上向右做匀加速直线运动,经3s钟撤去外力F.已知力F与水平方向的夹角θ=37°,sinθ=0.6,cosθ=0.8,g 取 10m/s2.试问:
如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上向右做匀加速直线运动,经3s钟撤去外力F.已知力F与水平方向的夹角θ=37°,sinθ=0.6,cosθ=0.8,g 取 10m/s2.试问: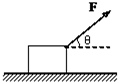 如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上向右做匀加速直线运动,经3s钟撤去拉力F.已知拉力F与水平方向的夹角θ=37°,sin37°=0.6,cos37°=0.8,取 g=10m/s2.求:
如图所示,木块的质量m=2kg,与地面间的动摩擦因数μ=0.2,木块在拉力F=10N作用下,在水平地面上向右做匀加速直线运动,经3s钟撤去拉力F.已知拉力F与水平方向的夹角θ=37°,sin37°=0.6,cos37°=0.8,取 g=10m/s2.求: