题目内容
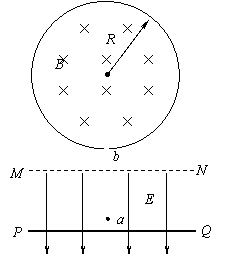 (16分)如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m。在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m=0.1g ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知
(16分)如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m。在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m=0.1g ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知![]() ,
,![]() )
)
⑴求出小球第一次与挡板PQ相碰后向上运动的距离;
⑵小球第一次从小洞b进入围栏时的速度大小;
⑶小球从第一次进入围栏到离开围栏经历的时间。
解析:
⑴设小球第一次与挡板相碰后向上运动距离为x1,则
qEd2 =0.8qEx1 (2分)
x1=1.25d2=6.25(cm) (2分)
⑵设第n次与挡板PQ相碰后向上运动距离为xn,则:
![]() (2分)
(2分)
要使小球能进入围栏,应有:
xn>d1+d2
综上:![]()
所以:当小球与挡板碰撞11次后,小球将第一次进入围栏内 (2分)
设进入速度大小为v,则应有:
![]() (2分)
(2分)
 解得:v=14(m/s) (1分)
解得:v=14(m/s) (1分)
⑶小球进入圆形围栏后,在洛伦兹力作用下做匀速圆周运动,如图所示
![]() 所以轨道半径
所以轨道半径 ![]() (m) (2分)
(m) (2分)
运动周期 ![]() (s)
(s)
图中 ![]() 所以 θ=30° (2分)
所以 θ=30° (2分)
即,当小球每转过120°圆周就与围栏碰撞一次,最终经过5次碰撞,从小洞b离开围栏区,故在围栏内运动时间为:
![]() (s) (1分)
(s) (1分)

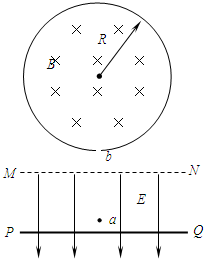 如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)
如图所示,直线MN的下方有竖直向下的匀强电场,场强大小为E=700V/m.在电场区域内有一个平行于MN的挡板PQ;MN的上方有一个半径为R=0.866m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=1.4T.围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm.现将一个质量为m=0.1g,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知1.2510=9.31,1.2511=11.628)
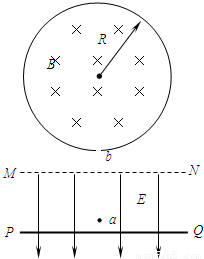
 m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.3T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m="0.1g" ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知
m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.3T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m="0.1g" ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知 ,
, )
)