题目内容
 如图所示,单摆摆球的质量为m,做简谐运动的周期为T,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v,不计空气阻力,则( )
如图所示,单摆摆球的质量为m,做简谐运动的周期为T,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v,不计空气阻力,则( )分析:由动能定理可求得重力所做的功;由单摆的周期可知A到B的时间;由功率公式可求得重力的功率;由动量定理可求得合力的冲量.
解答:解:A、从A到B的过程中,由动能定理可知,重力做功W=
mv2;故A正确;
B、从A到B的过程中时间为
,则重力做功的功率P=
,故B正确;
C、B点时由于重力竖直向下,而速度沿水平方向,故重力的功率为零,故C错误;
D、由动量定理可知,合力的冲量等于动量的变化量,故I=mv,故D正确;
故选ABD.
| 1 |
| 2 |
B、从A到B的过程中时间为
| T |
| 4 |
| 2mv2 |
| T |
C、B点时由于重力竖直向下,而速度沿水平方向,故重力的功率为零,故C错误;
D、由动量定理可知,合力的冲量等于动量的变化量,故I=mv,故D正确;
故选ABD.
点评:本题利用单摆考查了动能定理、动量定理及功率,综合性较强;要注意认真分析,合理利用所学过的物理规律进行解题.

练习册系列答案
相关题目
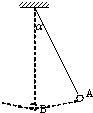 如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止开始释放,摆球运动到最低点B时的速度为v,已知重力加速度为g.则( )
如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止开始释放,摆球运动到最低点B时的速度为v,已知重力加速度为g.则( )A、摆球从A运动到B的过程中重力做功为
| ||
| B、摆球在A点时重力的瞬时功率为0 | ||
| C、摆球运动到B时重力的瞬时功率是mgv | ||
| D、摆球从A运动到B的过程中重力的瞬时功率不断增大 |
 如图所示,单摆摆球的质量为m,做简谐运动的周期为T,摆球从左侧最大位移A处(偏角θ<5°)由静止开始释放,不计空气阻力,摆球运动到最低点B时的速度为v,则下列说法正确的是( )
如图所示,单摆摆球的质量为m,做简谐运动的周期为T,摆球从左侧最大位移A处(偏角θ<5°)由静止开始释放,不计空气阻力,摆球运动到最低点B时的速度为v,则下列说法正确的是( )| A、摆球运动到B时加速度等于零 | ||
| B、摆球从A运动到B的过程中细线对小球拉力的冲量等于零 | ||
| C、摆球从A运动到B的过程中回复力的冲量大小等于mv | ||
D、摆球运动到最低点B时绳对其拉力比重力大
|
 如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v.重力加速度为g,不计空气阻力.则摆球从A运动到B的过程中( )
如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v.重力加速度为g,不计空气阻力.则摆球从A运动到B的过程中( )A、重力做的功为
| ||
| B、重力的最大瞬时功率为mgv | ||
| C、重力的冲量为0 | ||
| D、重力的冲量大小为mv |
 如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v.重力加速度为g,不计空气阻力.则摆球从A运动到B的过程中( )
如图所示,单摆摆球的质量为m,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v.重力加速度为g,不计空气阻力.则摆球从A运动到B的过程中( )