��Ŀ����
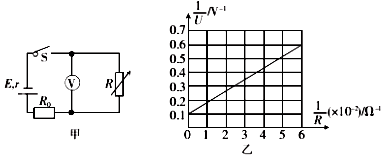
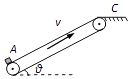
����Ŀ����ͼ���ף���ʾ��ƽ�й⻬��������ˮƽ���ã��������L=0.4m������һ������ֵR=0.3���ĵ���������������費�ƣ�����x��0һ�������x�����������ĺ㶨�ų����䷽���뵼��ƽ�洹ֱ���£��Ÿ�Ӧǿ��B��λ��x�仯��ͼ���ң���ʾ��һ������m=0.2kg������r=0.1���Ľ��������ڵ����ϣ����뵼�촹ֱ����������F�����´�x=0���Գ��ٶ�v0=2m/s�ص������ұ����˶����ҽ��������˶��������ܵ��İ�������С���䣮����˵������ȷ���ǣ� ��
A.�������������ȼ���ֱ���˶�
B.��������x=1 m�����ٶȴ�СΪ0.5m/s
C.��������x=0�˶���x=1m�����У�����F�����Ĺ�Ϊ��0.175 J
D.��������x=0�˶���x=2m�����У������������ĵ���Ϊ2C
���𰸡�B,C,D
���������⣺A������ͼ���B��x������ϵʽ��B=0.5+0.5x
�����������˶��и�Ÿ��߲�����Ӧ�綯��E=BLv
��Ӧ���� ![]()
������ ![]()
��ã� ![]() =
= ![]()
�����ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�� ![]() ��������ȱ���ֱ���˶���
��������ȱ���ֱ���˶��� ![]() ��x�����Թ�ϵ��������ʽ֪�����������������ȼ���ֱ���˶�����A����
��x�����Թ�ϵ��������ʽ֪�����������������ȼ���ֱ���˶�����A����
B������������������ܵİ�������С���䣬x=0����x=1����������С��ȣ��� ![]() ����
���� ![]() ����B��ȷ��
����B��ȷ��
C����������x=0���İ�������СΪ�� ![]() =0.2N
=0.2N
�Խ�������������x=0�˶���x=1m�����У����ݶ��ܶ����У�![]()
�������ݣ� ![]()
��ã� ![]() ����C��ȷ��
����C��ȷ��
D�����ݸ�Ӧ������ʽ ![]()
x=0��x=2�����У�B��xͼ���Χ�������Bx= ![]()
![]() ����D��ȷ
����D��ȷ
��ѡ��BCD
�����㾫����������Ĺؼ���������ܶ������ۺ�Ӧ�õ����֪ʶ������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��Լ������������⣬�˽ⰲ����������·���йأ��Ʊպϻ�·һ�ܣ����������Ĺ�����Ϊ��������Ϊ����Ҳ����Ϊ�㣬�����������͵糡������������Ϊ�㣮

 �ŵ������ϵ�д�
�ŵ������ϵ�д�