题目内容
(20分)一个“ ”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80T,如图所示,已知导轨ON段长为0.50m,电阻是0.40Ω,金属棒CD的电阻是0.20Ω,其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求:
”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80T,如图所示,已知导轨ON段长为0.50m,电阻是0.40Ω,金属棒CD的电阻是0.20Ω,其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求:

⑴导轨运动起来后,C、D两点哪点电势较高?
⑵导轨做匀速运动时,水平拉力F的大小是多少?
⑶导轨做匀加速运动的过程中,水平拉力F的最小值是多少?
⑷CD上消耗的电功率为P=0.80W时,水平拉力F做功的功率是多大?
(1)C;(2)2.48N;(3)1.6N;(4)6.72W。
【解析】
试题分析:(1)当导轨运动起来后,ON向左做切割磁感线的运动,由右手定则可判断出感应电流的方向由N到O,则对于CD来说,流过它的电流是由C到D,故C点的电势高于D点;
(2)由于导轨做匀速直线运动时,CD中的电流为4A,则导轨受到的安培力F=BIL=0.8T×4A×0.5m=1.6N,方向与拉力的方向相反;
另外导轨还受到向右的摩擦力,由于此时导体棒受到的安培力为F1= BIL=0.8T×4A×0.5m=1.6N,
导体棒对导轨的压力大小为mg-F1=0.6kg×10N/kg-1.6N=4.4N,
故导体棒受到的摩擦力的大小为f=4.4N×0.2=0.88N,
由于导轨处于匀速直线运动状态,故其受到的力平衡,则F=1.6N+0.88N=2.48N。
(3)设当导轨的速度为v时,水平拉力F′的值最小,故此时的ON受到的安培力大小等于CD受到的安培力大小,即
FON=BL×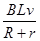 =
= ,方向向右;
,方向向右;
则CD棒受到的摩擦力的大小为f=(mg- )μ,
)μ,
由牛顿第二定律可得:F′-FON-f=Ma,
故F′=Ma+ +(mg-
+(mg- )μ=Ma+mgμ+(1-μ)×
)μ=Ma+mgμ+(1-μ)× ,
,
故当v=0时水平拉力F′的值最小,即F′=Ma+mgμ=2kg×0.2m/s2+0.6kg×10N/kg×0.2=1.6N。
(4)当CD上消耗的电功率为P=0.80W时,
根据电功率的计算公式可计算出导体棒上的电流I′=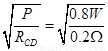 =2A,
=2A,
设导轨的速度为v′,则由感应电动势和欧姆定律得EON=I′(R+r)=BLv′
故v′=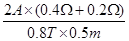 =3m/s;
=3m/s;
设此时的拉力为F拉,
则安培力的大小为F安=0.8T×0.5m×2A=0.8N,摩擦力的大小为(6N-0.8N)×0.2=1.04N,
由牛顿第二定律可得F拉-0.8N-1.04N=Ma=0.4N,故F拉=2.24N,
所以拉力的功率为P=F拉v′=2.24N×3m/s=6.72W。
考点:牛顿第二定律,欧姆定律,感应电动势,摩擦力,受力分析等知识。

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案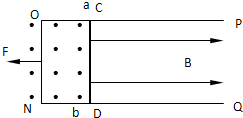 一个“U”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为M=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是?=020,CD棒与ON边平行,左边靠着光滑的固定立柱ab,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是B=0.80T,如图所示.已知导轨ON段长为L=0.50m,电阻是r=0.40Ω,金属棒CD的电阻是R=0.20Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以a=0.2m/s2做匀加速直线运动,一直到CD中的电流达到4A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求:
一个“U”形导轨PONQ,其质量为M=2.0kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为M=0.60kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是?=020,CD棒与ON边平行,左边靠着光滑的固定立柱ab,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是B=0.80T,如图所示.已知导轨ON段长为L=0.50m,电阻是r=0.40Ω,金属棒CD的电阻是R=0.20Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以a=0.2m/s2做匀加速直线运动,一直到CD中的电流达到4A时,导轨改做匀速直线运动.设导轨足够长,取g=10m/s2.求: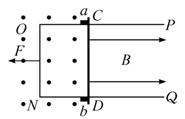

 ”形导轨PONQ,其质量为M=2.0 kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60
kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80 T,如图所示。已知导轨ON段长为0.50 m,电阻是0.40 Ω,金属棒CD的电阻是0.20 Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以0.20 m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0 A时,导轨改做匀速直线运动.设导轨足够长,取g=10 m/s2。求:
”形导轨PONQ,其质量为M=2.0 kg,放在光滑绝缘的水平面上,处于匀强磁场中,另有一根质量为m=0.60
kg的金属棒CD跨放在导轨上,CD与导轨的动摩擦因数是0.20,CD棒与ON边平行,左边靠着光滑的固定立柱a、b,匀强磁场以ab为界,左侧的磁场方向竖直向上(图中表示为垂直于纸面向外),右侧磁场方向水平向右,磁感应强度的大小都是0.80 T,如图所示。已知导轨ON段长为0.50 m,电阻是0.40 Ω,金属棒CD的电阻是0.20 Ω,其余电阻不计.导轨在水平拉力作用下由静止开始以0.20 m/s2的加速度做匀加速直线运动,一直到CD中的电流达到4.0 A时,导轨改做匀速直线运动.设导轨足够长,取g=10 m/s2。求: