题目内容
19.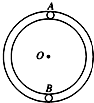 如图所示,光滑圆形管道固定在竖直面内,直径略小于管道内径可视为质点的小球A、B质量分别为mA、mB,A球从管道最高处由静止开始沿管道下滑,与静止于管道最低处的B球相碰,碰后A、B黏在一起且刚好到达与管道圆心O等高处,关于两小球质量比值$\frac{{m}_{A}}{{m}_{B}}$的说法正确的是( )
如图所示,光滑圆形管道固定在竖直面内,直径略小于管道内径可视为质点的小球A、B质量分别为mA、mB,A球从管道最高处由静止开始沿管道下滑,与静止于管道最低处的B球相碰,碰后A、B黏在一起且刚好到达与管道圆心O等高处,关于两小球质量比值$\frac{{m}_{A}}{{m}_{B}}$的说法正确的是( )| A. | $\frac{{m}_{A}}{{m}_{B}}$=$\sqrt{2}$+1 | B. | $\frac{{m}_{A}}{{m}_{B}}$=$\sqrt{2}$-1 | C. | $\frac{{m}_{A}}{{m}_{B}}$=1 | D. | $\frac{{m}_{A}}{{m}_{B}}$=$\sqrt{2}$ |
分析 碰后A、B球均能刚好到达与管道圆心O等高处,此时速度都为零,根据动能定理求出碰后AB两球的速度,碰撞前,A球从最高点运动到最低点的过程中,根据动能定理求出碰撞前A的速度,AB碰撞过程中,动量守恒,根据动量守恒定律求解即可.
解答 解:碰后A、B球均能刚好到达与管道圆心O等高处,则此时速度都为零,
根据动能定理可知,$mgR=\frac{1}{2}m{v}^{2}$,解得v=$\sqrt{2gR}$
当碰后A和B的速度相等,方向相同,${v}_{A}={v}_{B}=\sqrt{2gR}$,
碰撞前,A球从最高点运动到最低点的过程中,根据动能定理得:
$\frac{1}{2}{m}_{A}{{v}_{0}}^{2}={m}_{A}g•2R$
解得:${v}_{0}=\sqrt{4gR}$
AB碰撞过程中,动量守恒,以碰撞前A球的速度为正,则有:
mAv0=mAv共+mBv共
解得:$\frac{{m}_{A}}{{m}_{B}}$=$\sqrt{2}+1$,由上分析,故B正确,ACD错误;
故选:B.
点评 本题主要考查了动量守恒定律、动能定理的直接应用,解题时抓住碰后A、B球均能刚好到达与管道圆心O等高处求解,难度适中.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
9.关于两个分运动的合成,下列说法正确的有( )
| A. | 两匀速直线运动的合运动一定是匀速直线运动 | |
| B. | 两个直线运动的合运动一定是直线运动 | |
| C. | 合运动的速度一定大于两个分运动的速度 | |
| D. | 合运动的位移大小可能小于分运动的位移大小 |
7.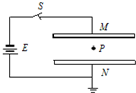 如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
 如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )
如图所示,两块相对的平行金属板M、N与电池相连,N板接电源正极并接地,板间的电场可视为匀强电场.在距离两板等远的一点P固定一个带负电的点电荷,则( )| A. | 保持S闭合,将N板向下移,则P点的电势升高 | |
| B. | 保持S闭合,将N板向下移,则点电荷的电势能增大 | |
| C. | 将S断开,使N板向下移,则P点的电势减小 | |
| D. | 将S断开,使N板向下移,则点电荷的电势能减小 |
14.某人用脚把质量1kg的球以水平速度10m/s踢出,球在地面上滚动50m停下,在这个过程中,重力对球以及人对球所做的功分别为( )
| A. | 0、0 | B. | 0、50J | C. | 50J、500J | D. | 500J、0 |
4.下列说法正确的是( )
| A. | 电容器是一种储存电荷的装置 | B. | 避雷针是用来防止静电的 | ||
| C. | 电感器应用了电流的热效应 | D. | 电磁炉应用了电磁感应现象 |
8.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步,下列表述正确的是( )
| A. | 法拉第发现了电流的磁效应. | |
| B. | 库仑提出了库仑定律,并最早用实验测得元电荷e的数值 | |
| C. | 伽利略发现了行星运动的规律,并通过实验测出了引力常量 | |
| D. | 荷兰科学家昂尼斯(或昂纳斯)发现大多数金属在温度降到某一值时,都会出现电阻突然降为零的现象--超导现象 |
9.在如图所示电路中,电源的电动势为E,内阻为r,当变阻器R2的滑动触头P向b端移动时( )


| A. | 电压表示数变大,电流表示数变小 | B. | 电压表示数变小,电流表示数变大 | ||
| C. | 电压表示数变大,电流表示数变大 | D. | 电压表示数变小,电流表示数变小 |
