题目内容
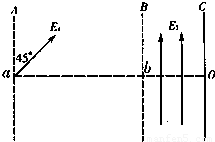
如图所示，AB间存在方向与竖直成45°角斜向上的匀强电场E1，BC间存在竖直向上的匀强电场E2，AB间距为0.2m，BC间距离为0.1m，C为荧光屏，质量m=1.0×10-3kg，电量q=+1.0×10-2C的带电粒子由a点静止释放，恰好沿水平方向经过b点到达荧光屏的O点，若在BC间再加方向垂直纸面向外大小B=1.0T的匀强磁场，粒子经b点偏转到达荧光屏的O′点（未画出）．取g=10m/s2．求：
（1）E1的大小
（2）加上磁场后，粒子由b到点O′点电势能的变化量．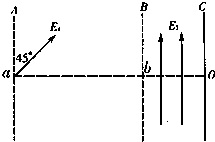
（1）E1的大小
（2）加上磁场后，粒子由b到点O′点电势能的变化量．
（1）粒子在AB间作匀加速直线运动，受力如图，
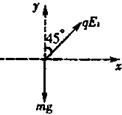
qE1cos45°=mg…①
E1=
=
=1.4v/m…②
（2）由动能定理得：qE1sin45°?dAB=
m
…③
vb=
=
=2m/s…④
加磁场前粒子在BC间作匀速直线运动
则有qE2=mg…⑤
加磁场后粒子作匀速圆周运动，轨迹如图．
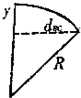
由牛顿第二定律得：qvbB=
，R=
=0.2m．…⑥
设偏转距离为y，由几何关系得：R2=dBC2+(R-y)2…⑦
解得：y=2.7×10-2m…⑧
W=-qE2?y=-mgy=-2.7×10-4J…⑨
即电势能变化了2.7×10-4J…⑩
答：（1）E1的大小为1.4V/m；
（2）加上磁场后，粒子由b到点O′点电势能的变化量2.7×10-4J．
qE1cos45°=mg…①
E1=
| mg |
| qcos45° |
| 2 |
（2）由动能定理得：qE1sin45°?dAB=
| 1 |
| 2 |
| v | 2b |
vb=
|
| 2gdAB |
加磁场前粒子在BC间作匀速直线运动
则有qE2=mg…⑤
加磁场后粒子作匀速圆周运动，轨迹如图．
由牛顿第二定律得：qvbB=
m
| ||
| R |
| mvb |
| qB |
设偏转距离为y，由几何关系得：R2=dBC2+(R-y)2…⑦
解得：y=2.7×10-2m…⑧
W=-qE2?y=-mgy=-2.7×10-4J…⑨
即电势能变化了2.7×10-4J…⑩
答：（1）E1的大小为1.4V/m；
（2）加上磁场后，粒子由b到点O′点电势能的变化量2.7×10-4J．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
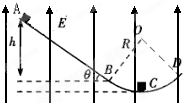如图所示，AB是一倾角为θ=37°的绝缘粗糙直轨道，滑块与斜面间的动摩擦因数μ=0.30，BCD是半径为R=0.2m的光滑圆弧轨道，它们相切于B点，C为圆弧轨道的最低点，整个空间存在着竖直向上的匀强电场，场强E=4.0×103N/C，质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下．已知斜面AB对应的高度h=0.24m，滑块带电荷q=-5.0×10-4C，取重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80．求：
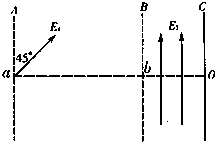（2007?潍坊模拟）如图所示，AB间存在方向与竖直成45°角斜向上的匀强电场E1，BC间存在竖直向上的匀强电场E2，AB间距为0.2m，BC间距离为0.1m，C为荧光屏，质量m=1.0×10-3kg，电量q=+1.0×10-2C的带电粒子由a点静止释放，恰好沿水平方向经过b点到达荧光屏的O点，若在BC间再加方向垂直纸面向外大小B=1.0T的匀强磁场，粒子经b点偏转到达荧光屏的O′点（未画出）．取g=10m/s2．求：
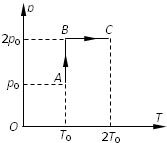A、（选修模块3-3）