题目内容
17．
如图所示，为粗细均匀的两端开口向上的细U形管，管水平部分长L，管中装有某种液体，静止时液面在同一水平面上．当以加速度a向右做匀加速运动时，左侧液面高，左右两管中液面的高度差是$\frac{La}{g}$．（水平管内始终有液体）
分析 高度差产生压强差，压强差乘以液面面积等于力差，力差产生了水平部分那些液体（质量为LSp）的加速度
解答 解：根据牛顿第二定律知，细管以及细管中的液体具有向右的加速度，对细管底端取一小段液体，可知左边的压力大于右边的压力，左侧液面高，
设水平部分那些液体的质量m=LSp，设高度差为△h，则：
pg△hS=LSpa
得：△h=$\frac{La}{g}$
故答案为：左；$\frac{La}{g}$
点评 本题考查的比较巧妙，解决本题的关键通过一小段水的受力确定出细管的加速度方向，从而确定出细管的运动规律．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
一列简谐波在t=0时刻的波形图线如图所示，质点P向下振动，若波速为3m/s，在原图上画出t=1.5s时的波形图（至少画出一个波长）．
12．
质量为M的球用长为L的悬线固定于O点，在O点正下方$\frac{L}{2}$处有一颗钉子，把悬线拉直与竖直方向成一定角度，由静止释放小球，如图所示，当悬线碰到钉子时，下列说法正确的是（ ）
质量为M的球用长为L的悬线固定于O点，在O点正下方$\frac{L}{2}$处有一颗钉子，把悬线拉直与竖直方向成一定角度，由静止释放小球，如图所示，当悬线碰到钉子时，下列说法正确的是（ ）| A． | 小球的机械能突然减少 | B． | 小球的向心加速度突然增大 | ||
| C． | 小球的角速度突然减小 | D． | 悬线的张力突然增大 |
2．
固定的光滑斜面倾角为37°，AB两个物块通过轻细线连接跨过定滑轮，如图所示，开始时让物块A静止在斜面底端，B离地面高为h，连接A物块的细线与斜面平行，A物块的质量为m，B物块的质量为M，不计滑轮质量及细线与滑轮间的摩擦，释放A物块后，A在B物块的带动下沿斜面上滑，B物块与地面碰撞后不反弹，则（ ）
固定的光滑斜面倾角为37°，AB两个物块通过轻细线连接跨过定滑轮，如图所示，开始时让物块A静止在斜面底端，B离地面高为h，连接A物块的细线与斜面平行，A物块的质量为m，B物块的质量为M，不计滑轮质量及细线与滑轮间的摩擦，释放A物块后，A在B物块的带动下沿斜面上滑，B物块与地面碰撞后不反弹，则（ ）| A． | A物块的最大速度为$\sqrt{\frac{2（M-m）gh}{（m+M）}}$ | |
| B． | A物块的最大速度为$\sqrt{\frac{2（5M-3m）gh}{5（m+M）}}$ | |
| C． | A物块沿斜面上升的最大位移为$\frac{2（4M-m）}{3（m+M）}$h | |
| D． | A物块沿斜面上升的最大位移为$\frac{8Mh}{3（M+m）}$ |
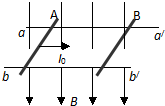如图所示，aa′、bb′为在同一水平面内的两条相距为d的平行长直金属导轨，其上平行地静置有两根可在导轨上无摩擦滑动的金属棒A和B，两金属棒的质量均为m，电阻均为R，棒与导轨接触良好，其他电阻不计，两导轨间有磁感应强度为B的匀强磁场，其方向垂直轨道平面竖直向下．今在极短时间对金属棒A施加一个水平向右的冲量I0，从而使两棒在导轨平面上运动，最终A、B两棒恰能相碰．在整个过程中，求：
如图为某质点做直线运动的v-t图，由图可知该质点在3s时加速度是0m/s2，在8s时加速度是1.5m/s2，在12s时加速度是-4.5m/s2．
如图所示，斜面体固定在水平地面上，斜面体顶端有一轻滑轮，跨过滑轮的轻细绳一端与放在光滑斜面上的物块A相连，另一端与物块B相连．已知物块A的质量为m，物块B的质量为2m，开始时物块B离地面的高度为h，重力加速度为g，斜面足够长，现把物块A由静止释放，求：