题目内容
16．
如图所示，传送带以恒定速率v运动，现将质量都是m的小物体甲、乙（视为质点）先后轻放在传送带的最左端，甲到达A处时恰好达到速率v，乙到达B处时恰好达到速率v．在甲、乙两物体在传送带上加速的过程中，下列说法正确的是（ ）| A． | 两物体的加速度相同 | |
| B． | 两物体的加速时间不同 | |
| C． | 传送带对两物体做功相等 | |
| D． | 乙在传送带上滑行系统产生的热量与甲在传送带上滑行系统产生的热量相等 |
分析 根据运动学过程分析可知二得运动的加速度和时间关系；再由动能定理即可明确传送带做功情况
解答 解：A、两物体在传送带上达到最大速度经过的位移不同，则由v2=2ax，可知说明二者的加速度不同，时间t=$\frac{v}{a}$，则加速时间也不同；故A错误，B正确；
C、由动能定理可知，传送带对甲、乙两物体做功等于动能的改变量，故说明传送带做功相等，故C正确；
D、对于任一物体，加速度 a=$\frac{μmg}{m}$=μg，从放上传送带到与传送带共速的时间 t=$\frac{v}{a}$，物体与传送带的相对位移△x=vt-$\frac{vt}{2}=\frac{{v}^{2}}{2μg}$，可知△x相等，产生的热量 Q=μmg△x，所以产生的热量相等，故D正确．
故选：BCD．
点评 本题考查传送带问题的分析，要注意明确物体在传送带上的运动过程，明确动能定理及牛顿第二定律的应用．
练习册系列答案
阅读快车系列答案
相关题目
11．从高为h的阳台上以初速度v0水平抛出一物体，在某一时刻物体的速度为v1，则此时物体的高度为（ ）
| A． | $\frac{{v}_{0}^{2}}{2g}$+h-$\frac{{v}_{1}^{2}}{2g}$ | B． | $\frac{{v}_{0}^{2}}{2g}$+$\frac{{v}_{1}^{2}}{2g}$ | ||
| C． | $\frac{{v}_{0}^{2}}{2g}$+h+$\frac{{v}_{1}^{2}}{2g}$ | D． | $\frac{{v}_{0}^{2}}{2g}$-$\frac{{v}_{1}^{2}}{2g}$ |
4．
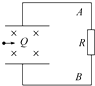磁流体发电机可以把气体的内能直接转化为电能，是一种低碳环保发电机，有着广泛的发展前景，其发电原理示意图如图所示，将一束等离子体（即高温下电离的气体，含有大量带正电和负电的微粒，整体上呈电中性）喷射入磁感应强度为B的匀强磁场中，磁场区域有两块面积为S、相距为d的平行金属板与外电阻R相连构成一电路．设气流的速度为v，气体的电导率（电阻率的倒数）为g，则（ ）
磁流体发电机可以把气体的内能直接转化为电能，是一种低碳环保发电机，有着广泛的发展前景，其发电原理示意图如图所示，将一束等离子体（即高温下电离的气体，含有大量带正电和负电的微粒，整体上呈电中性）喷射入磁感应强度为B的匀强磁场中，磁场区域有两块面积为S、相距为d的平行金属板与外电阻R相连构成一电路．设气流的速度为v，气体的电导率（电阻率的倒数）为g，则（ ）| A． | 两板间的电势差为U=Bdv | |
| B． | 下板是电源的负极，上板是电源的正极 | |
| C． | 流经R的电流为I=$\frac{Bdv}{R}$ | |
| D． | 流经R的电流为I=$\frac{BdvSg}{gSR+d}$ |
1．
某制药厂的污水处理站的管道中安装了如图所示的流量计，该装置由绝缘材料制成，长、宽、高分别为a、b、c，左右两端开口，在垂直于上下底面方向加磁感应强度为B的匀强磁场，在前后两个面的内侧固定有金属板作为电极，当含有大量正负离子（其重力不计）的污水充满管口从左向右流经该装置时，利用电压表所显示的两个电极间的电压U，就可测出污水流量Q（单位时间内流出的污水体积）．则下列说法正确的是（ ）
某制药厂的污水处理站的管道中安装了如图所示的流量计，该装置由绝缘材料制成，长、宽、高分别为a、b、c，左右两端开口，在垂直于上下底面方向加磁感应强度为B的匀强磁场，在前后两个面的内侧固定有金属板作为电极，当含有大量正负离子（其重力不计）的污水充满管口从左向右流经该装置时，利用电压表所显示的两个电极间的电压U，就可测出污水流量Q（单位时间内流出的污水体积）．则下列说法正确的是（ ）| A． | 后表面的电势一定高于前表面的电势，与正负哪种离子多少无关 | |
| B． | 若污水中正负离子数相同，则前后表面的电势差为零 | |
| C． | 流量Q越大，两个电极间的电压U越小 | |
| D． | 污水中离子数越多，两个电极间的电压U越大 |
2．某汽车由静止开始做匀加速直线运动，加速度为5m/s2，10秒内的位移（ ）
| A． | 25m | B． | 250m | C． | 500m | D． | 1000m |