题目内容

(10分)如图所示，半径为R的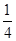光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点．

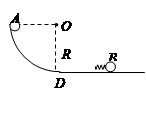
求：（1）小球A滑到圆弧面底端时的速度大小．
（2）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少．
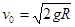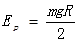
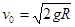（1）     （2） 

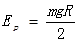
试题分析：（1）设A球到达圆弧底端时的速度为v0，由机械能守恒定律有：
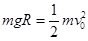   ①（2分）    
A球到达圆弧底端时的速度 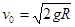    ②（2分）
（2）当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v（1分）
由动量守恒定律有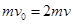：  ③（2分）    
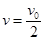得   ④（1分）
由能量守恒可知，弹簧的最大弹性势能
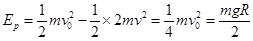 ⑤（2分）
练习册系列答案
相关题目
（19分）如图所示，在倾角为θ的光滑斜面上，有一长为l的细线，一端固定在O点，另一端拴一质量为m的小球．现使小球恰好能在斜面上做完整的圆周运动，已知O点到斜面底边的距离sOC＝L，求：
 
(1)小球通过最高点A时的速度vA.
(2)小球通过最低点B时，细线对小球的拉力．
(3)小球运动到A点或B点时细线断裂，小球滑落到斜面底边时到C点的距离若相等，则l和L应满足什么关系？
能量的形式有多种并且通过做功会发生相互转化。如下图所示，在光滑水平面上，子弹m水平射入木块后留在木块内。现将子弹、弹簧、木块合在一起作为研究对象，则此系统从子弹开始射入木块到弹簧压缩到最短的整个过程中，则系统的
 
A．子弹与木块有摩擦阻力，能量不守恒，机械能不守恒
B．子弹与木块有摩擦阻力，但能量和机械能均守恒
C．子弹与木块有摩擦阻力，但能量守恒，机械能不守恒
D．能量不守恒，机械能守恒
（1）（6分）氢原子的能级如图所示。氢原子从n=3能级向n=l能级跃迁所放出的光子，恰能使某种金属产生光电效应，则该金属的截止频率为____Hz；用一群处n=4能级的氢原子向低能级跃迁时所发出的光照射该金属，产生的光电子最大初动能为____ eV（普朗克常量h=6．63×10-34J'·s，结果均保留2位有效数字）。

（2）（9分）如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内．a、b是轨道的两端点且高度相同，O为圆心。小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰。第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）。求A、B两球的质量之比mA:mB。（结果可以用根式表示）
如图所示，高为h的光滑斜面固定在水平地面上。一质量为m的小物块，从斜面顶端A由静止开始下滑。重力加速度为g，不计空气阻力。求：

（1）小物块从斜面顶端A滑到底端B的过程中重力做的功W;
（2）小物块滑到底端B时速度的大小v。
如右图所示，物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧，物体A、B的质量分别为m、2m，开始时细绳伸直，用手托着物体A使弹簧处于原长且A与地面的距离为h，物体B静止在地面上．放手后物体A下落，与地面即将接触时速度为v，此时物体B对地面恰好无压力，则下列说法中正确的是(　　)

A．物体A下落过程中的任意时刻，加速度不会为零
B．此时弹簧的弹性势能等于mgh＋mv2
C．此时物体B处于平衡状态
D．此过程中物体A的机械能变化量为mgh＋mv2
奥运会中的投掷的链球、铅球、铁饼和标枪等体育比赛项目都是把物体斜向上抛出的运动，这些物体从抛出到落地的过程中（不计空气阻力）：
A．物体的机械能一直减小
B．物体的机械能不变
C．物体的动能先增大后减小，重力势能先减小后增大
D．物体的动能先减小后增大，重力势能先增大后减小
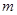如图所示，质量均为的两个物体甲和乙从同一水平面下降相同高度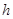，甲物体竖直向下运动，乙物体沿斜面下滑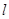。下列说法正确的是
A．重力对甲做功B．重力对乙做功
C．甲的重力势能增加D．乙的重力势能减小
下列关于机械能是否守恒的叙述正确的是（    ）
A．做匀速直线运动的物体，机械能一定守恒
B．做匀变速直线运动的物体，机械能一定守恒
C．做匀变速曲线运动的物体，机械能一定不守恒
D．做匀速圆周运动的物体，机械能不一定守恒

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网