题目内容
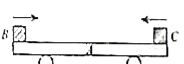
【题目】如图,空间有一竖直向下沿x轴方向的静电场,电场的场强大小按E=kx分布(x是轴上某点到O点的距离),![]() .x轴上,有一长为L的绝缘细线连接A、B两个小球,两球质量均为m,B球带负电,带电量为 q,A球距O点的距离为L。两球现处于静止状态,不计两球之间的静电力作用。
.x轴上,有一长为L的绝缘细线连接A、B两个小球,两球质量均为m,B球带负电,带电量为 q,A球距O点的距离为L。两球现处于静止状态,不计两球之间的静电力作用。
(1)求A球的带电量qA;
(2)将A、B间细线剪断,描述B球的运动情况,并分析说明理由;
(3)剪断细线后,求B球的最大速度vm.

【答案】(1)qA=-4q (2)B球做往复运动 (3)vm=![]()
【解析】
(1)A、B两球静止时,A球所处位置场强为
![]()
B球所处位置场强为
![]()
对A、B由整体受力分析,由平衡条件可得:
![]()
解得:
qA=-4q
(2)剪断细线后,B球初始受到合力
F=mg-![]() mg=
mg=![]() mg
mg
方向竖直向下,B球开始向下运动;
运动后,B球受力为
F合=mg-kxq,
随x增大,F合减小,所以B球做加速度减小的加速运动;
当F合减小为零时,B球速度达到最大,继续向下运动,F合方向向上,并逐渐增大,B球做加速度增大的减速运动。
当速度减小为零后,此时电场力大于重力,B球反向运动,最终B球做往复运动。
(3)当B球下落速度达到最大时,B球距O点距离为x0
![]()
解得:
x0=3L
当B球下落速度达到最大时,B球距O点距离为3L
运动过程中,电场力大小线性变化,所以对B球下落到速度最大过程由动能定理得:
![]()
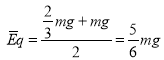
解得:
vm=![]()

 走进文言文系列答案
走进文言文系列答案【题目】小明同学通过实验探究某一金属电阻的阻值R随温度t的变化关系,已知该金属电阻在常温下的阻值约10 Ω,R随t的升高而增大,实验电路如图所示,控温箱用以调节金属电阻的温度。

实验时闭合S,先将开关K与1端闭合,调节金属电阻的温度,分别记下温度t1,t2,…和电流表的相应示数I1,I2,…。然后将开关K与2端闭合,调节电阻箱使电流表的示数再次为I1,I2,…,分别记下电阻箱相应的示数R1,R2,…。
(1)有以下两电流表,实验电路中应选用________。
A.量程0~100 mA,内阻约2 Ω
B.量程0~0.6 A,内阻可忽略
(2)实验过程中,要将电阻箱的阻值由9.9 Ω调节至10.0 Ω,需旋转图中电阻箱的旋钮“a”、“b”、“c”,正确的操作顺序是________。
①将旋钮a由“0”旋转至“1”
②将旋钮b由“9”旋转至“0”
③将旋钮c由“9”旋转至“0”
(3)实验记录的t和R的数据见下表
温度t(℃) | 20.0 | 40.0 | 60.0 | 80.0 | 100.0 |
阻值R(Ω) | 9.6 | 10.4 | 11.1 | 12.1 | 12.8 |
请根据表中数据,在答题卡的方格纸上作出R-t图线。
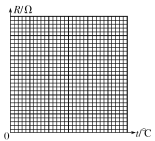
由图线求得R随t的变化关系为R=________Ω。