题目内容
9. 一轻弹簧的左端固定在墙壁上,右端自由,一质量为m=1kg的滑块从距弹簧右端L0=1.2m的P点以初速度v0=4m/s正对弹簧运动,如图所示,滑块与水平面的动摩擦因数为?=0.2,在与弹簧碰后反弹回来,归终停止在距P点为L1=0.8m的Q点,求:
一轻弹簧的左端固定在墙壁上,右端自由,一质量为m=1kg的滑块从距弹簧右端L0=1.2m的P点以初速度v0=4m/s正对弹簧运动,如图所示,滑块与水平面的动摩擦因数为?=0.2,在与弹簧碰后反弹回来,归终停止在距P点为L1=0.8m的Q点,求:(1)在滑块与弹簧碰撞过程中弹簧最大压缩量为多少?
(2)弹簧的最大弹性势能为多少?
分析 滑块在水平面上滑动,对滑块应用动能定理可以求出弹簧的最大压缩量、与最大弹性势能.
解答 解:设弹簧最大压缩量为x,在滑块向左运动的过程中,由动能定理可得:
-μmg(x+L0)-EP=0-$\frac{1}{2}$mv02…①
在滑块返回的过程中,由动能定理得:EP-μmg(x+L0+L1)=0…②
代入数据,由①②解得:x=0.4m,EP=4.8J;
答:(1)在滑块与弹簧碰撞过程中弹簧最大压缩量为0.4m;
(2)弹簧的最大弹性势能为4.8J.
点评 本题考查了动能定理的应用,分析清楚滑块的运动过程是正确解题的前提与关键,分析清楚运动过程后,应用动能定理即可正确解题;解题时,也可以对全程应用动能定理答题,对整个过程,由动能定理列式求解.

练习册系列答案
相关题目
19.在做“用油膜法估测分子的大小”的实验中,备有下列器材:油酸酒精溶液、滴管、痱子粉、浅盘及水、玻璃板、彩笔.还缺少的器材是( )
| A. | 只有量筒 | B. | 只有坐标纸 | C. | 量筒和坐标纸 | D. | 不再缺少仪器 |
20. 用一水平力将小球从最低点缓慢拉到图所示位置的过程中,关于水平拉力与绳的弹力的合力,下列判断正确的是( )
用一水平力将小球从最低点缓慢拉到图所示位置的过程中,关于水平拉力与绳的弹力的合力,下列判断正确的是( )
 用一水平力将小球从最低点缓慢拉到图所示位置的过程中,关于水平拉力与绳的弹力的合力,下列判断正确的是( )
用一水平力将小球从最低点缓慢拉到图所示位置的过程中,关于水平拉力与绳的弹力的合力,下列判断正确的是( )| A. | 合力大小逐渐增大 | B. | 合力大小逐渐变小 | ||
| C. | 合力方向逐渐向右偏 | D. | 合力方向保持竖直向上不变 |
17. 如图所示,竖直放置在水平面上的轻弹簧上叠放着两物块A、B,A、B质量均为5kg,它们处于静止状态,若突然将一个大小为25N,方向竖直向下的力施加在物体A上,则在此瞬间A对B的压力大小为(g=10m/s2)( )
如图所示,竖直放置在水平面上的轻弹簧上叠放着两物块A、B,A、B质量均为5kg,它们处于静止状态,若突然将一个大小为25N,方向竖直向下的力施加在物体A上,则在此瞬间A对B的压力大小为(g=10m/s2)( )
 如图所示,竖直放置在水平面上的轻弹簧上叠放着两物块A、B,A、B质量均为5kg,它们处于静止状态,若突然将一个大小为25N,方向竖直向下的力施加在物体A上,则在此瞬间A对B的压力大小为(g=10m/s2)( )
如图所示,竖直放置在水平面上的轻弹簧上叠放着两物块A、B,A、B质量均为5kg,它们处于静止状态,若突然将一个大小为25N,方向竖直向下的力施加在物体A上,则在此瞬间A对B的压力大小为(g=10m/s2)( )| A. | 25N | B. | 10N | C. | 62.5N | D. | 30N |
14. 一简谐波沿x轴的正方向以5m/s的波速在弹性绳上传播,波的振幅为0.4m,在t时刻波形如图所示,从此刻开始再经过0.3s,则( )
一简谐波沿x轴的正方向以5m/s的波速在弹性绳上传播,波的振幅为0.4m,在t时刻波形如图所示,从此刻开始再经过0.3s,则( )
 一简谐波沿x轴的正方向以5m/s的波速在弹性绳上传播,波的振幅为0.4m,在t时刻波形如图所示,从此刻开始再经过0.3s,则( )
一简谐波沿x轴的正方向以5m/s的波速在弹性绳上传播,波的振幅为0.4m,在t时刻波形如图所示,从此刻开始再经过0.3s,则( )| A. | 质点Q正处于波峰 | B. | 振源的周期为0.3s | ||
| C. | 质点Q通过的总路程为1.2m | D. | 质点M正处于波峰 |
1.先后用两种不同的单色光,在相同的条件下用同双缝干涉装置做实验,在屏幕上相邻的两条亮纹间距不同,其中间距较大的那种单色光,比另一种单色光( )
| A. | 在真空中的波长较短 | |
| B. | 在玻璃中传播的速度较大 | |
| C. | 在玻璃中传播时,玻璃对其折射率较大 | |
| D. | 其在空气中传播速度大 |
19.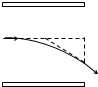 如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )
如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )
 如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )
如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )| A. | 若粒子的运动轨迹相同,说明它们具有相同的初动能 | |
| B. | 比荷大的粒子,在射出电场时,其速度偏向角一定大 | |
| C. | 若粒子在电场中的运动时间相等,则它们的初速度一定相等 | |
| D. | 在电场中运动时间越长的粒子,电场力对它做的功越多 |

