题目内容
质量为m的小球，用一条绳子系在竖直平面内做圆周运动，小球到达最高点时的速度为v，到达最低点时的速变为
，则两位置处绳子所受的张力之差是（ ）
| 4gR+v2 |
分析：在最高点，小球受重力和绳子的拉力T1，合力提供向心力；在最低点，重力和拉力T2，合力也提供向心力；根据牛顿第二定律列式后联立求解即可．
解答：解：在最高点，小球受重力和绳子的拉力T1，合力提供向心力，根据牛顿第二定律，有：
mg+T1=m
①
在最低点，重力和拉力T2，合力提供向心力，根据牛顿第二定律，有：
T2-mg=m
②
最低点速度为：v′=
③
两位置处绳子所受的张力之差为：△T=T2-T1 ④
联立解得：△T=6mg
故选A．
mg+T1=m
| v2 |
| R |
在最低点，重力和拉力T2，合力提供向心力，根据牛顿第二定律，有：
T2-mg=m
| v′2 |
| R |
最低点速度为：v′=
| 4gR+v2 |
两位置处绳子所受的张力之差为：△T=T2-T1 ④
联立解得：△T=6mg
故选A．
点评：本题关键是明确在最高点和最低点小球的合力提供向心力，然后根据牛顿第二定律列式求解出两个拉力，得到拉力之差．
练习册系列答案
相关题目
如图所示，一质量为m的小球，用一根长为L的细绳悬挂于O点，在O正下方O′处有一钉子．将小球拉到P处后释放，当它摆到最低点P′时，悬线被钉子挡住，在绳与钉子相碰的瞬间，下列说法正确的是（ ）
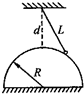如图所示，质量为m的小球，用一根长为L的绳吊起来，放在半径为R光滑球体表面上，由悬点到球面的最小距离为d，则小球对球面的压力和绳的拉力各为多少？
（2006?盐城模拟）如图所示，质量为M的滑块B套在光滑的水平杆上可自由滑动，质量为m的小球A用一长为L的轻杆与B上的O点相连接，轻杆处于水平位置，可绕O点在竖直面内自由转动．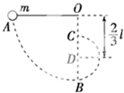
如图所示，质量为m的小球，用一长为l的细线悬于O点，将悬线拉直成水平状态，并给小球一个向下的速度让小球向下运动，O点正下方D处有一钉子，小球运动到B处时会以D为圆心做圆周运动，并经过C点，若已知OD=