题目内容
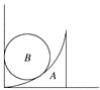
【题目】如图所示,一小球从平台上水平抛出,恰好落在平台前一倾角为α=53°的斜面顶端并刚好沿斜面下滑,已知平台到斜面顶端的高度为h=0.8 m,不计空气阻力,取g=10 m/s2.(sin 53°=0.8,cos 53°=0.6)求:
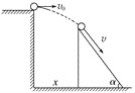
(1)小球水平抛出的初速度v0;
(2)斜面顶端与平台边缘的水平距离x.
【答案】(1)3 m/s (2)1.2 m
【解析】试题分析:(1) 小球水平抛出后做平抛运动,由高度h可求出小球到达斜面顶端时竖直分速度.因为小球刚好能沿光滑斜面下滑,说明此时小球的速度的方向恰好沿着斜面的方向,由速度的分解可以求得初速度的大小;
(2) 根据平抛运动的规律可以求得接触斜面之前的水平方向的位移,即为斜面顶端与平台边缘的水平距离。
解:(1) 小球水平抛出后做平抛运动,设刚到达斜面顶端时竖直分速度的大小为vy,水平分速度为v0,合速度为v1
由vy2=2gh得,![]()
由题意可知:小球落到斜面顶端刚好沿光滑斜面下滑,说明此时小球速度方向与斜面平行,所以 vy=v0tan53°
解得:![]() ;
;
(2) 由vy=gt1
解得:平抛运动的时间![]()
所以水平距离 s=v0t1=3×0.4m=1.2m。
点晴:小球在接触斜面之前做的是平抛运动,在斜面上时小球做匀加速直线运动,根据两个不同的运动的过程,分段求解即可。

练习册系列答案
相关题目