题目内容
如图中虚线所示为静电场的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV时,它的动能应为( )
A.8eV
B.13eV
C.20eV
D.34eV
【答案】分析:要求正电荷的电势能为-8ev时的动能,需要知道该正电荷的动能和电势能的总和,得出Eka+Epa=Ekb+Epb,得出Epb-Epa=21ev从而确定φb>φa;根据电荷经过a、b点的动能分别为26eV和5eV和ab之间有两个等势面且等势面3的电势为0,可设等势面4的电势为φ,则等势面a的电势-2φ,再根据该正电荷的动能和电势能的总和保持不变求出正电荷的动能.
解答:解:在只有电场力做功的条件下动能和电势能的总和保持不变,故有Eka+Epa=Ekb+Epb…①
所以26ev+Epa=5ev+Epb
Epb-Epa=26ev-5ev=21ev…②
根据EP=qφ可知φb>φa,
由于相邻等势面之间的电势差相同,
等势面3的电势为0,设等势面4的电势为φ,则等势面a的电势-2φ,
代入②式得qφ-(-2qφ)=3qφ=21ev
qφ=7ev
正电荷的能量故有Ek+(-8ev)=5ev+7ev
EK=5ev+7ev+8ev=20ev
故C正确,
故选C.
点评:“在只有电场力做功的条件下动能和电势能的总和保持不变;相邻等势面之间的电势差相同”是我们解决此类问题时的突破口.
解答:解:在只有电场力做功的条件下动能和电势能的总和保持不变,故有Eka+Epa=Ekb+Epb…①
所以26ev+Epa=5ev+Epb
Epb-Epa=26ev-5ev=21ev…②
根据EP=qφ可知φb>φa,
由于相邻等势面之间的电势差相同,
等势面3的电势为0,设等势面4的电势为φ,则等势面a的电势-2φ,
代入②式得qφ-(-2qφ)=3qφ=21ev
qφ=7ev
正电荷的能量故有Ek+(-8ev)=5ev+7ev
EK=5ev+7ev+8ev=20ev
故C正确,
故选C.
点评:“在只有电场力做功的条件下动能和电势能的总和保持不变;相邻等势面之间的电势差相同”是我们解决此类问题时的突破口.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 (2003?北京)如图中虚线所示为静电场的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV时,它的动能应为( )
(2003?北京)如图中虚线所示为静电场的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV时,它的动能应为( )
 、
、 点时的动能分别为26eV和5eV,当这一点电荷运动到某一位置,其电势能变为
点时的动能分别为26eV和5eV,当这一点电荷运动到某一位置,其电势能变为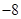 eV时,它的动能应为(
)
eV时,它的动能应为(
)
