Question

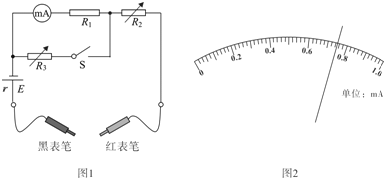
【题目】某空间存在着变化的电场和另一个变化的磁场，电场方向向右，即如图中b点到c点的方向，电场强度大小变化如图中E—t图象；磁场强度变化如图中B—t所示.在a点从t=0开始每隔2s有一个相同的带电粒子沿ab方向以速度v射出(第1s末射出第一个粒子)，这些粒子都恰能击中c点，若ab垂直于bc，ac=2bc，粒子重力不计，且粒子在ac段运动时间小于1s，求

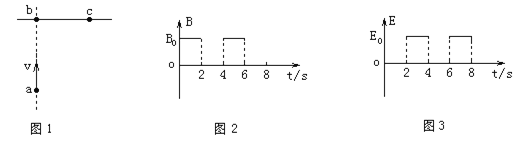
(1)图中E0与B0的比值；

(2)两次带电粒子击中c点的速度之比；

(3)若以第一个粒子击中c点的时刻为(1+△t)s，那么第2个粒子击中c点的时刻为多少？

Answer 1

【答案】(1)(2) (3)

【解析】

(1)设ac=2bc=2L．在t=1s时，空间区域只存在匀强磁场，粒子做匀速圆周运动，洛伦兹力提供向心力．由牛顿第二定律得：

由图可知，

R=ac=2L．

则

当粒子在电场中运动时，在ab方向上是匀速运动，在bc方向上是匀加速运动，则有

得：

由上述式得

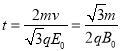
(2)第一次粒子在磁场中做匀速圆周运动，则击中c点的速度为v；
第二次粒子在电场中运动击中c点时，沿bc方向的速度：

则合速度：

则两次带电粒子击中c点的速度之比:

(3)第一个粒子击中c点的时刻已知为（1+△t）s，该粒子是在磁场中运动，所需时间是由其轨迹对应的圆心角所确定的，由图可知粒子从a到c时，轨迹的圆心角为，所以

可得：

并将其代入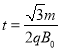，可得第二个粒子在电场中运动的时间为：

，

故第二个粒子击中c点的时刻为：

．