Question

已知氘核的质量为2．0136u，中子质量为1．0087u，氦3(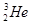)的质量为3．0150u。两个氘核聚变生成氦3的反应方程是_________；聚变放出的能量是________；若两个氘核以相同的动能Ek＝0．35MeV正碰，则碰撞后生成物的动能为__________,____________。（假设核反应中的能量都转化为粒子的动能）

Answer 1

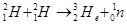(1)                （1分）
(2)3.26MeV          （2分）
(3)中子：2.97MeV，氦核：0.99MeV.

解析考点：动量守恒定律；爱因斯坦质能方程．
分析：（1）要写出核反应方程，必须知道生成物是什么，所以可以根据核反应过程遵循质量数守恒和核电荷数守恒求出新核的质量数、核电荷数从而确定新核，并最终写出核反应方程式．要计算计算释放的核能，就必须知道核反应亏损的质量，根据爱因斯坦质能方程△E=△mC²即可求出核反应释放的能量．
（2）根据动量守恒定律及能力守恒定律即可求解．
解：（1）聚变的核反应方程：2₁²H→₂³He+₀¹n
核反应过程中的质量亏损为△m=2m_D-（m_He+m_n）=0.0035u
释放的核能为△E=△mc²=0.0035uc²="3.26MeV"
（2）对撞过程动量守恒，由于反应前两氘核动能相同，其动量等值反向，因此反应前后系统的动量为0．即：
0=m_Hev_He+m_nv_n，
反应前后总能量守恒，得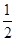：m_Hev_He²+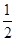m_nv_n²=△E+2E_k0，
解得：E_kn=2.97Mev， E_kHe=0.99Mev．
故答案为：(1)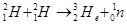
(2)3.26MeV          
(3)中子：2.97MeV，氦核：0.99MeV.