题目内容
 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为| 3 | 5 |
(1)碰撞后的瞬间A、B、C的速度各是多少?
(2)最终A、B、C的速度又是多少?
(3)要使C完全离开B并不脱离木板A,每块木板的长度应满足什么条件?
分析:(1)由动能定理研究A列出等式,A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律列出等式求解碰撞后的速度.
(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,由动量守恒定律列出等式求解最终A、B、C的速度.
(3)对于AB整体运用动能定理列出等式结合几何关系求解木板的长度应满足的条件.
(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,由动量守恒定律列出等式求解最终A、B、C的速度.
(3)对于AB整体运用动能定理列出等式结合几何关系求解木板的长度应满足的条件.
解答:解:(1)一开始A与水平地面之间的滑动摩擦力f1=μmg,A向右加速运动.
由动能定理得:(F-f1)s=
mv12…①
A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,
由动量守恒定律得:m v1=(m+m)v2…②
由①②解得:v2=2m/s.
A、B碰撞过程时间极短,所以C此时的速度为0.
A、B、C的速度是2m/s,2m/s,0.
(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,AB整体、C受滑动摩擦力分别为f2=3μmg、f3=μmg,
选三个物体构成的整体为研究对象,外力之和为零,则:
2mv2=(2m+m)v3 …③.
①②③联立得:v3=
,
再代入数据可得v3=
m/s…④
所以最终A、B、C的速度是
m/s
(3)设AB整体、C向前移动的位移分别为s1、s2,对于AB整体运用动能定理有:
(F-f2)s1-f3s1=
×2mv32-
×2mv22,
对于C:f3s2=
mv32…⑤
C相对于AB的位移为s3,由几何关系得:s3+s2=s1…⑥
由②③④⑤⑥解得:s3=
s=
m.
要使C完全离开B,C相对于A的位移
L≤s3=
m
要使C不脱离木板A,则:
L≥s3,
解得:L≥
m.
要使C完全离开B并不脱离木板A,每块木板的长度应满足
m≤L≤
m
答:(1)碰撞后的瞬间A、B、C的速度各是2m/s,2m/s,0.
(2)最终A、B、C的速度又是
m/s.
(3)要使C完全离开B并不脱离木板A,每块木板的长度应满足
m≤L≤
m.
由动能定理得:(F-f1)s=
| 1 |
| 2 |
A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,
由动量守恒定律得:m v1=(m+m)v2…②
由①②解得:v2=2m/s.
A、B碰撞过程时间极短,所以C此时的速度为0.
A、B、C的速度是2m/s,2m/s,0.
(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,AB整体、C受滑动摩擦力分别为f2=3μmg、f3=μmg,
选三个物体构成的整体为研究对象,外力之和为零,则:
2mv2=(2m+m)v3 …③.
①②③联立得:v3=
| 2 |
| 3 |
| μgs |
再代入数据可得v3=
| 4 |
| 3 |
所以最终A、B、C的速度是
| 4 |
| 3 |
(3)设AB整体、C向前移动的位移分别为s1、s2,对于AB整体运用动能定理有:
(F-f2)s1-f3s1=
| 1 |
| 2 |
| 1 |
| 2 |
对于C:f3s2=
| 1 |
| 2 |
C相对于AB的位移为s3,由几何关系得:s3+s2=s1…⑥
由②③④⑤⑥解得:s3=
| 1 |
| 3 |
| 2 |
| 3 |
要使C完全离开B,C相对于A的位移
L≤s3=
| 2 |
| 3 |
要使C不脱离木板A,则:
| 3 |
| 2 |
解得:L≥
| 4 |
| 9 |
要使C完全离开B并不脱离木板A,每块木板的长度应满足
| 4 |
| 9 |
| 2 |
| 3 |
答:(1)碰撞后的瞬间A、B、C的速度各是2m/s,2m/s,0.
(2)最终A、B、C的速度又是
| 4 |
| 3 |
(3)要使C完全离开B并不脱离木板A,每块木板的长度应满足
| 4 |
| 9 |
| 2 |
| 3 |
点评:本题关键通过受力分析,明确各个物体的运动情况,运用动量守恒定律和动能定理综合列式求解.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
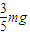 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.