题目内容
如图所示,三块木板A、B、C的质量均为m,长度均为L,A、B置于水平地面上,它们的间距s=2米。C置于B板的上端并对齐。A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力。开始时,三个物体处于静止状态。现给A施加一个水平向右,大小为(1)碰撞后的瞬间A、B、C的速度是多少?
(2)碰撞后C相对于A板静止时,A、B、C的速度是多少?
(3)求开始碰撞到C相对于A板静止时A的位移。
 | |
(1)一开始A与水平地面之间的滑动摩擦力f1=μmg,A向右加速运动。 由动能定理得 (F-f1)s=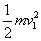 ①A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得 m v1=(m+m)v2 ②A、B、C的速度是2m/s 2m/s 0(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,设AB整体、C向前移动的位移分别为S1、s2,受滑动摩擦力分别为f2=3μmg、f3=μmg, 选三个物体构成的整体为研究对象,外力之和为零,则 2mv2=(2m+m)v3 ③解①②③得v3=
①A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得 m v1=(m+m)v2 ②A、B、C的速度是2m/s 2m/s 0(2)碰撞结束后到三个物体达到共同速度的相互作用过程中,设AB整体、C向前移动的位移分别为S1、s2,受滑动摩擦力分别为f2=3μmg、f3=μmg, 选三个物体构成的整体为研究对象,外力之和为零,则 2mv2=(2m+m)v3 ③解①②③得v3=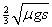 ,再代入数据可得v3=
,再代入数据可得v3=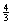 m/s ④所以最终A、B、C的速度是
m/s ④所以最终A、B、C的速度是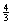 m/s(3)S=10/9 m
m/s(3)S=10/9 m

练习册系列答案
相关题目
 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
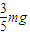 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.