题目内容
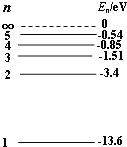
【题目】如图所示,边长为L的正方形金属框,质量为m,电阻为R,用细线把它悬挂于一个有界的匀强磁场边缘,金属框的上半部处于磁场内,下半部处于磁场外.磁场随时间变化规律为B=kt(k>0),已知细线所能承受的最大拉力为2mg,求:
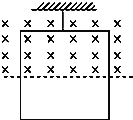
(1)线圈的感应电动势大小;
(2)细绳拉力最大时,导体棒受到的安培力大小;
(3)从t=0开始直到细线会被拉断的时间.
【答案】(1)线圈的感应电动势大小为k![]() .
.
(2)细绳拉力最大时,导体棒受到的安培力大小为mg.
(3)从t=0开始直到细线会被拉断的时间为![]() .
.
【解析】
试题分析:(1)根据法拉第电磁感应定律,通过磁感应强度的变化率求出感应电动势的大小.
(2)根据左手定则判断出安培力的方向,结合共点力平衡求出细绳拉力最大时,导体棒所受的安培力大小.
(3)根据安培力的大小,通过安培力的大小公式求出细绳被拉断所需的时间.
解:(1)由磁场随时间变化规律为B=kt(k>0)得:![]() =k
=k
根据法拉第电磁感应定律有:E=![]() S=k
S=k![]() .
.
(2)当细线刚要断时,根据共点力平衡有:T=F安+mg
解得:F安=T﹣mg=2mg﹣mg=mg.
(3)根据闭合电路欧姆定律得:I=![]() =
=![]() ,B=kt
,B=kt
由第(1)问知,当拉力等于安培力时,绳子断裂,则有:mg=![]()
解得:t=![]() .
.
答:(1)线圈的感应电动势大小为k![]() .
.
(2)细绳拉力最大时,导体棒受到的安培力大小为mg.
(3)从t=0开始直到细线会被拉断的时间为![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目