题目内容
16.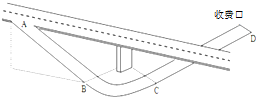 清明节高速免费,物理何老师驾车在返城经过高速公路的一个出口路段如图所示,发现轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到收费口D点停下.已知轿车在出口A处的速度v0=20m/s,AB长L1=200m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=10m/s,轮胎与BC段路面间的动摩擦因μ=0.2,最大静摩擦力可认为等于滑动摩擦力,CD段为平直路段长L2=100m,重力加速度g取10m/s2.
清明节高速免费,物理何老师驾车在返城经过高速公路的一个出口路段如图所示,发现轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到收费口D点停下.已知轿车在出口A处的速度v0=20m/s,AB长L1=200m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=10m/s,轮胎与BC段路面间的动摩擦因μ=0.2,最大静摩擦力可认为等于滑动摩擦力,CD段为平直路段长L2=100m,重力加速度g取10m/s2.求:(1)若轿车到达B点速度刚好为v=10m/s,轿车在AB下坡段加速度的大小;
(2)为保证行车安全,车轮不打滑,水平圆弧段BC半径R的最小值
(3)轿车A点到D点全程的最短时间.
分析 (1)轿车在AB段做匀减速直线运动,已知初速度、位移和末速度,根据速度位移关系公式求解加速度.
(2)轿车在BC段做匀速圆周运动,由静摩擦力充当向心力,为保证行车安全,车轮不打滑,所需要的向心力不大于最大静摩擦力,据此列式求解半径R的最小值.
(3)分三段,分别由运动学公式求解时间,即可得到总时间
解答 解:(1)对AB段匀减速直线运动有:
${v}^{2}-{{v}_{0}}^{2}$=-2aL1
代入数据解得:a=0.75m/s2
(2)汽车在BC段做圆周运动,静摩擦力提供向心力,有:
$f=m\frac{{v}^{2}}{R}$
为了确保安全,则须满足 Ff≤μmg
联立解得:R≥50m,即:Rmin=50m
(3)设AB段时间为t1,BC段时间为t2,CD段时间为t3,全程所用最短时间为t.
L1=$\frac{{v}_{0}+v}{2}{t}_{1}$
$\frac{1}{2}$πR=vt2
L2=$\frac{v}{2}{t}_{3}$
总时间为:t=t1+t2+t3
解得:t=41.18 s
答:(1)若轿车到达B点速度刚好为v=36km/h,轿车在AB下坡段加速度的大小为0.75m/s2;
(2)为保证行车安全,车轮不打滑,水平圆弧段BC半径R的最小值为50m;
(3)轿车A点到D点全程的最短时间为41.18 s
点评 本题是运动学与动力学综合题,能结合物体的运动情况,灵活选择运动学的公式形式是关键,当不涉及加速度而要求时间时,可用位移等于平均速度乘以时间来求.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
6.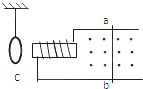 如图所示,铜制闭合线圈c被轻线竖直悬吊于天花板上,当金属导轨上的导体棒ab在匀强磁场中沿导轨运动时(导轨电阻不计),下列说法正确的是( )
如图所示,铜制闭合线圈c被轻线竖直悬吊于天花板上,当金属导轨上的导体棒ab在匀强磁场中沿导轨运动时(导轨电阻不计),下列说法正确的是( )
 如图所示,铜制闭合线圈c被轻线竖直悬吊于天花板上,当金属导轨上的导体棒ab在匀强磁场中沿导轨运动时(导轨电阻不计),下列说法正确的是( )
如图所示,铜制闭合线圈c被轻线竖直悬吊于天花板上,当金属导轨上的导体棒ab在匀强磁场中沿导轨运动时(导轨电阻不计),下列说法正确的是( )| A. | ab向右做匀速运动时闭合线圈c将被螺线管吸引 | |
| B. | ab向右做减速运动时闭合线圈c将被螺线管吸引 | |
| C. | ab向左做匀速运动时闭合线圈c将被螺线管排斥 | |
| D. | ab向左做加速运动时闭合线圈c将被螺线管吸引 |
7.100mL水与100mL酒精混合后体积小于200mL,这时因为( )
| A. | 物质分子之间有一定间隔 | B. | 物质混合后分子变小了 | ||
| C. | 混合后形成新的分子 | D. | 混合后分子的质量变小 |
11.通过近三年的学习,同学们已经掌握了许多物理知识,请你用所学物理知识判断下列四个具体物理问题,你认为下列处理方法或者观点没有明显错误的是( )
| A. | 宇航员驾驶宇宙飞船以接近光速经过地球时,地球上的人观察到飞船上的时钟变快 | |
| B. | 两个半径均为r的空心金属球,带电量均为+Q,均置于绝缘基座上,球心相距3r,两球间的库仑力小于k$\frac{{{q_1}{q_2}}}{{9{r^2}}}$ | |
| C. | 在高压输电过程中是不会产生电磁波的 | |
| D. | 人在下蹲过程中,地面对人的支持力做负功,导致人的机械能减少 |
1.某人以拉力F将物体沿斜面向上拉,如图所示,拉力等于摩擦力(即F=Ff),则下列说法正确的是( )
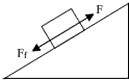

| A. | 物体匀速运动 | B. | 物体的机械能不变 | ||
| C. | 拉力的瞬时功率不变 | D. | 物体的机械能增大 |
3.一矩形线圈在匀强磁场中匀速转动,产生正弦式交流电,当线圈平面与中性面垂直时,下面说法正确的是( )
| A. | 电流方向将发生改变 | B. | 磁通量的变化率达到最大值 | ||
| C. | 通过线圈的磁通量达到最大值 | D. | 线圈所受磁场力达到最大值 |
4.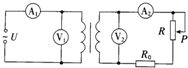 如图是通过降压变压器给用户供电的示意图.变压器的输入电压是市电电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器滑片P向下移动时,下列说法不正确的是( )
如图是通过降压变压器给用户供电的示意图.变压器的输入电压是市电电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器滑片P向下移动时,下列说法不正确的是( )
 如图是通过降压变压器给用户供电的示意图.变压器的输入电压是市电电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器滑片P向下移动时,下列说法不正确的是( )
如图是通过降压变压器给用户供电的示意图.变压器的输入电压是市电电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器滑片P向下移动时,下列说法不正确的是( )| A. | 相当于增加用电器数目 | |
| B. | A1表的示数随A2表的示数增大而增大 | |
| C. | 变压器的输入功率增加 | |
| D. | V1表的示数随V2表的示数的增大而增大 |
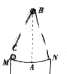 如图所示,光滑的弧形槽的半径为R(R远大于弧长MN),A为弧形槽的最低点,M、N点等高,小球C放在M点.小球B放在A点正上方,同时释放两球,使两球正好在A点相碰,则小球C去到到A的时间t=(2n+1)$\frac{π}{2}$$\sqrt{\frac{l}{g}}$(n=0,1,2,3…),小球B距A点的高度为h=h=$\frac{1}{8}$π2(2n+1)2R (n=0,1,2,3…).(重力加速度为g)
如图所示,光滑的弧形槽的半径为R(R远大于弧长MN),A为弧形槽的最低点,M、N点等高,小球C放在M点.小球B放在A点正上方,同时释放两球,使两球正好在A点相碰,则小球C去到到A的时间t=(2n+1)$\frac{π}{2}$$\sqrt{\frac{l}{g}}$(n=0,1,2,3…),小球B距A点的高度为h=h=$\frac{1}{8}$π2(2n+1)2R (n=0,1,2,3…).(重力加速度为g)