题目内容
 如图所示,一个内壁光滑的细管弯成半径为R的半圆形轨道CD,竖直放置,其内径略大于小球的直径,水平轨道与竖直半圆轨道在C点连接完好.置于水平轨道上的弹簧左端与竖直墙壁相连,B处为弹簧的自然状态.将一个质量为m的小球放在弹簧的右侧后,用力向左侧推小球而压缩弹簧至A处,然后将小球由静止释放,小球刚好能运动到D处.水平轨道以B处为界,左侧AB段长x=R,与小球的动摩擦因数为μ,右侧BC段光滑.求:
如图所示,一个内壁光滑的细管弯成半径为R的半圆形轨道CD,竖直放置,其内径略大于小球的直径,水平轨道与竖直半圆轨道在C点连接完好.置于水平轨道上的弹簧左端与竖直墙壁相连,B处为弹簧的自然状态.将一个质量为m的小球放在弹簧的右侧后,用力向左侧推小球而压缩弹簧至A处,然后将小球由静止释放,小球刚好能运动到D处.水平轨道以B处为界,左侧AB段长x=R,与小球的动摩擦因数为μ,右侧BC段光滑.求:(1)小球运动到轨道C点时对轨道的压力
(2)弹簧在压缩时所储存的弹性势能.
分析:(1)小球到达D处时速度为零时,小球刚好能运动到D处,由动能定理或机械能守恒定律可以求出小球在C处的速度;小球在圆形轨道内做圆周运动,由牛顿第二定律可以求出小球在C点时受到的支持力,然后求出小球对轨道的压力.
(2)由能量守恒定律可以求出弹簧在压缩时储存的弹性势能.
(2)由能量守恒定律可以求出弹簧在压缩时储存的弹性势能.
解答:解:(1)从C到D过程中,由动能定理得:-mg?2R=0-
mvC2 ①,
在C点,由牛顿第二定律得:F-mg=m
,
解得:F=5mg,由牛顿第三定律得:
小球对的、轨道的压力F′=F=5mg;
(2)从A到C过程中,由能量守恒定律可得:
EP=μmgR+
mvC2 ②,
由①②解得:EP=(μ+2)mgR;
答:(1)小球运动到轨道C点时对轨道的压力为5mg;
(2)弹簧在压缩时所储存的弹性势能为(μ+2)mgR.
| 1 |
| 2 |
在C点,由牛顿第二定律得:F-mg=m
| ||
| R |
解得:F=5mg,由牛顿第三定律得:
小球对的、轨道的压力F′=F=5mg;
(2)从A到C过程中,由能量守恒定律可得:
EP=μmgR+
| 1 |
| 2 |
由①②解得:EP=(μ+2)mgR;
答:(1)小球运动到轨道C点时对轨道的压力为5mg;
(2)弹簧在压缩时所储存的弹性势能为(μ+2)mgR.
点评:小球刚好到达圆管形轨道最高点的条件是:到达最高点时速度为零;应用动能定理、牛顿第二定律、能量守恒定律即可正确解题.

练习册系列答案
相关题目
 在实验室做了一个这样的光学实验,即在一个密闭的暗箱里依次放上小灯泡(紧靠暗箱的左内壁)、烟熏黑的玻璃、狭缝、针尖、感光胶片(紧靠暗箱的右内壁),整个装置如图所示,小灯泡发出的光通过熏黑的玻璃后变得十分微弱,经过三个月的曝光,在感光胶片上针头影子周围才出现非常清晰的衍射条纹.对感光胶片进行了光能量测量,得出每秒到达感光胶片的光能量是5×10-13J.假如起作用的光波波长约为500nm,且当时实验测得暗箱的长度为1.2m,若光子依次通过狭缝,普朗克常量h=6.63×10-34J?s.求:
在实验室做了一个这样的光学实验,即在一个密闭的暗箱里依次放上小灯泡(紧靠暗箱的左内壁)、烟熏黑的玻璃、狭缝、针尖、感光胶片(紧靠暗箱的右内壁),整个装置如图所示,小灯泡发出的光通过熏黑的玻璃后变得十分微弱,经过三个月的曝光,在感光胶片上针头影子周围才出现非常清晰的衍射条纹.对感光胶片进行了光能量测量,得出每秒到达感光胶片的光能量是5×10-13J.假如起作用的光波波长约为500nm,且当时实验测得暗箱的长度为1.2m,若光子依次通过狭缝,普朗克常量h=6.63×10-34J?s.求: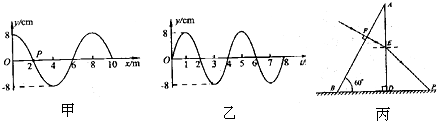


 ,该球体对蓝光的折射率为
,该球体对蓝光的折射率为 .则它从球面射出时的出射角β=___________;若换用一束紫光同样从A点射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置__________(填“偏左”、“偏右”或“不变”).
.则它从球面射出时的出射角β=___________;若换用一束紫光同样从A点射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置__________(填“偏左”、“偏右”或“不变”).

 发生衰变有多种可能性.其中的一种可能是,
发生衰变有多种可能性.其中的一种可能是, ,再经一次衰变变成
,再经一次衰变变成 (X代表某种元素),或再经一次衰变变成
(X代表某种元素),或再经一次衰变变成 和
和 最后都衰变成
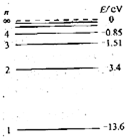
最后都衰变成 ,衰变路径如图所示,则由图可知:①②③④四个过程中________是α衰变;______是β衰变.
,衰变路径如图所示,则由图可知:①②③④四个过程中________是α衰变;______是β衰变.


 ,该球体对蓝光的折射率为
,该球体对蓝光的折射率为 .则它从球面射出时的出射角β=___________;若换用一束紫光同样从A点射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置__________(填“偏左”、“偏右”或“不变”).
.则它从球面射出时的出射角β=___________;若换用一束紫光同样从A点射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置__________(填“偏左”、“偏右”或“不变”).

 发生衰变有多种可能性.其中的一种可能是,
发生衰变有多种可能性.其中的一种可能是, ,再经一次衰变变成
,再经一次衰变变成 (X代表某种元素),或再经一次衰变变成
(X代表某种元素),或再经一次衰变变成 和
和 最后都衰变成
最后都衰变成 ,衰变路径如图所示,则由图可知:①②③④四个过程中________是α衰变;______是β衰变.
,衰变路径如图所示,则由图可知:①②③④四个过程中________是α衰变;______是β衰变.
