Question

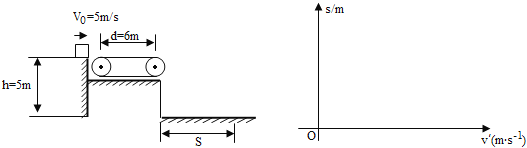
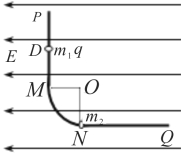
【题目】如图所示的竖直平面内有范围足够大、水平向左的匀强电场,电场强度为E．一绝缘弯杆由两段直杆和一半径R=1．6m的四分之一圆弧杆MN组成,固定在竖直面内,两直杆与圆弧杆的连接点分别是M、N,竖直杆PM和水平杆NQ均足够长,PMN段光滑．现有一质量为m1=0．2kg、带电荷量为+q的小环1套在PM杆上,从M点的上方的D点静止释放,恰好能达到N点．已知q=2×10C, E=2×102N/m, g取10m/s2．

（1）求D、M间的距离h1=?

（2）求小环1第一次通过圆弧杆上的M点时,圆弧杆对小环作用力F的大小?

（3）在水平杆NQ上的N点套一个质量为m2=0．6kg、不带电的小环2,小环1和2与NQ间的动摩擦因数μ=0．1．现将小环1移至距离M点上方h2=14．4m处由静止释放,两环碰撞后,小环2在NQ上通过的最大距离是s2=8m．两环间无电荷转移．环与杆之间的最大静摩擦力等于滑动摩擦力．经过足够长的时间,问小环1的状态?并求小环1在水平杆NQ上运动通过的总路程S1

Answer 1

【答案】（1）1．6m （2）8N （3）8m

【解析】

试题分析：（1）小环由D到N，由动能定理有m1g（h1+R）-qER=0

解得h1=R

h1=1．6 m

（2）设小环由D到M点时速度为vm，则m1gh1＝m1vm2

FqE＝m1

解得F=qE+2m1g

F=8N

（3）设小环1从h2=9R处由静止释放后，到达N点的速度为v0，碰撞后小环1和2的速度分别是v1和v2，则m2gμs2＝m2v22

m1g（h2+R）qER＝m1v02

mv0=m1v1+m2v2

v1=4 m/s

小环1碰撞后向右运动，水平方向受向左的电场力和滑动摩擦力，停止后又将向左运动，回到N点速度大于零，沿竖直轨道运动，将超过D点，以后如此做往复运动，每次回到N点速度越来越小，最后等于零，将不会在水平杆NQ上运动．

小环1的最后状态是：在D、N两点之间做往复运动．

m1v12＝μm1gs1

s1=8 m